Questões de Concurso
Filtrar
131 Questões de concurso encontradas
Página 13 de 27
Questões por página:
Questões por página:
Uma variável x tem distribuição normal com média 5 e desvio padrão igual a 3. Já a variável y também tem distribuição normal, mas com média 10 e desvio padrão igual a 4. Sabe-se que x e y são independentes. A variável z = x + y tem distribuição
O coeficiente de determinação (R2) e o desvio-padrão σ podem ser estimados através das estatísticas 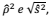 respectivamente. Contudo, esses estimadores tenderão a apresentar alguns problemas de tal forma que:
respectivamente. Contudo, esses estimadores tenderão a apresentar alguns problemas de tal forma que:
O número de policiais assassinados nas cidades brasileiras tem despertado a preocupação dos especialistas. Para uma amostra de 16 cidades, a média mensal de policiais mortos foi de 12. Embora discreta, supõe-se que tal variável possa ser aproximada por uma Normal, sobre a qual é sabido que:
Ø(1,28) = 0,9, Ø(1,64)= 0,95 e Ø(1,96)= 0,975
onde Ø é a função distribuição acumulada da normal padrão.
Se o desvio padrão verdadeiro do número de óbitos é dado, igual a seis, é correto afirmar que:
O conjunto de dados abaixo exibe uma amostra de 5 entrevistados que informaram seu peso e sua idade.

Assinale a alternativa que contém o desvio-padrão ( ) do peso dos entrevistados com 20 anos.
) do peso dos entrevistados com 20 anos.

Assinale a alternativa que contém o desvio-padrão (
 ) do peso dos entrevistados com 20 anos.
) do peso dos entrevistados com 20 anos.
Concurso:
AL-RO
Disciplina:
Estatística
Há 5 meses, sua empresa fez um contrato para vender exclusivamente o trigo produzido por uma cooperativa. Seu fornecedor informa que não poderá fazer entrega nos próximos dois meses (mês 6 e mês 7). Em função dessa descontinuidade, o gerente geral de sua empresa pede para você calcular a previsão da soma das demandas dos dois meses citados. Ele o orientou a simplificar os cálculos, optando por uma projeção baseada em uma regressão linear que usa os dados das demandas dos 5 meses desde o início da venda de trigo. Os dados estão apresentados, mês a mês, na tabela a seguir.
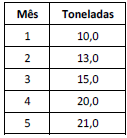
Assim, após fazer os cálculos segundo essas orientações, o resultado correto para a soma pedida é

Assim, após fazer os cálculos segundo essas orientações, o resultado correto para a soma pedida é