Questões de Concurso
Filtrar
132 Questões de concurso encontradas
Página 14 de 27
Questões por página:
Questões por página:
Concurso:
AL-RO
Disciplina:
Estatística
Há 5 meses, sua empresa fez um contrato para vender exclusivamente o trigo produzido por uma cooperativa. Seu fornecedor informa que não poderá fazer entrega nos próximos dois meses (mês 6 e mês 7). Em função dessa descontinuidade, o gerente geral de sua empresa pede para você calcular a previsão da soma das demandas dos dois meses citados. Ele o orientou a simplificar os cálculos, optando por uma projeção baseada em uma regressão linear que usa os dados das demandas dos 5 meses desde o início da venda de trigo. Os dados estão apresentados, mês a mês, na tabela a seguir.
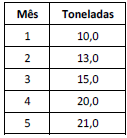
Assim, após fazer os cálculos segundo essas orientações, o resultado correto para a soma pedida é

Assim, após fazer os cálculos segundo essas orientações, o resultado correto para a soma pedida é
Concurso:
AL-RO
Disciplina:
Estatística
mostrar texto associado
Obtidos corretamente os valores de SQE, SQD e SQT, o valor da estatística de teste F será dado por
Concurso:
AL-RO
Disciplina:
Estatística
mostrar texto associado
Os valores de a, b e c são respectivamente:
Concurso:
AL-RO
Disciplina:
Estatística
Para testar H0: µ ≤ 20 contra H1: µ > 20, em que µ é a média de uma distribuição normal com variância desconhecida, uma amostra aleatória de tamanho 16 foi observada e exibiu as estatísticas a seguir.

Com base nesses dados, o valor da estatística de teste t-Student usual, a regra de decisão a ela associada ao nível de significância de 5% e a decisão são, respectivamente,
Concurso:
AL-RO
Disciplina:
Estatística
mostrar texto associado
O estimador não tendencioso de variância uniformemente mínima de µ é
