Questões de Concurso
Filtrar
101 Questões de concurso encontradas
Página 3 de 21
Questões por página:
Questões por página:
Concurso:
Instituto Federal Pará
Disciplina:
Estatística
Com o objetivo de verificar se há independência entre a área do curso de graduação (Ciências Exatas, Ciências da Natureza e Ciências Humanas) e o sexo dos estudantes (Feminino e Masculino), um professor de uma instituição de ensino superior coletou os dados apresentados na tabela a seguir:
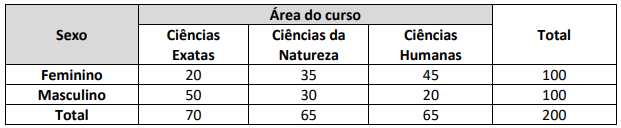
Nesse contexto, denote: • X = número esperado, sob a suposição de independência, de estudantes do sexo Feminino que escolheram um curso na área de Ciências Exatas;
• Y = graus de liberdade da estatística do teste qui-quadrado associado.
Com base nos dados fornecidos, os valores de X e Y são, respectivamente:
Nesse contexto, denote: • X = número esperado, sob a suposição de independência, de estudantes do sexo Feminino que escolheram um curso na área de Ciências Exatas;
• Y = graus de liberdade da estatística do teste qui-quadrado associado.
Com base nos dados fornecidos, os valores de X e Y são, respectivamente:
Concurso:
Prefeitura de Juiz de Fora - MG
Disciplina:
Estatística
No teste da hipótese de que a variância de uma população é igual ao valor fixo σ02 ,
ou seja, H0 : σ2 = σ02, usa-se a estatística
em que s2 é a estimativa da variância calculada com base em uma amostra composta por n observações. Essa estatística possui uma distribuição qui-quadrado com certo número de graus de liberdade. Foi aplicado um teste para a hipótese citada em uma amostra com 15 observações. Então, é correto afirmar que a esperança matemática (média) e a variância de uma variável aleatória com a distribuição descrita são, respectivamente,
Concurso:
Prefeitura de Cuiabá - MT
Disciplina:
Estatística
No programa R, as funções dnorm(), pnorm(), qnorm() e rnorm() com os respectivos parâmetros para a distribuição normal, retorna tais valores, respectivamente:
Concurso:
Universidade do Estado do Pará (UEPA)
Disciplina:
Estatística
ALERT: Essa questão ainda está sendo revisada pela equipe FonteConcursos!
Concurso:
Universidade do Estado do Pará (UEPA)
Disciplina:
Estatística
Considere as seguintes afirmações:
I. as distribuições de Bernoulli e Binomial apresentam as mesmas características e, portanto, os mesmos parâmetros;
II. repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de “sucesso”, dão origem ao modelo Binomial;
III. o Teorema do Limite Central garante que, para n suficientemente grande, a distribuição de Bernoulli pode ser aproximada pela distribuição de Poisson.
Pode-se afirmar que
I. as distribuições de Bernoulli e Binomial apresentam as mesmas características e, portanto, os mesmos parâmetros;
II. repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de “sucesso”, dão origem ao modelo Binomial;
III. o Teorema do Limite Central garante que, para n suficientemente grande, a distribuição de Bernoulli pode ser aproximada pela distribuição de Poisson.
Pode-se afirmar que
