Questões de Concurso
Filtrar
101 Questões de concurso encontradas
Página 5 de 21
Questões por página:
Para testar a variância de uma medida, um estatístico resolve usar a distribuição Qui-Quadrado, dadas as probabilidades:
As hipóteses são as seguintes:
Ho: σ2 = 15 contra Ha: σ2 ≠ 15
A partir de uma amostra com 11 observações, conclui-se que:
abaixo: 
Em um determinado ramo de atividade, os salários dos empregados são normalmente distribuídos com média igual a R$ 3.600,00. Se 60% dos empregados ganham um salário inferior a R$ 3.700,00, então,35% dos empregados ganham um salário de no máximo
Avalie se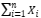 
é uma estatística suficiente para o parâmetro indicado nos casos a seguir.
I. Uma distribuição Bernoulli para a qual o parâmetro p (0 < p < 1) é desconhecido.
II. Uma distribuição geométrica para a qual o parâmetro p (0 < p < 1) é desconhecido.
III. Uma distribuição normal com média conhecida e variância σ2 desconhecida.
Está correto o que se afirma em
Avalie se as seguintes famílias de distribuições são uma família exponencial:
I. A família de distribuições Poisson com média desconhecida.
II. A família de distribuições normais com média conhecida e variância desconhecida.
III. A família de distribuições Beta com parâmetro α conhecido e parâmetro β desconhecido.
IV. A família de distribuições Uniforme no intervalo (0, θ), θ parâmetro desconhecido.
São de fato famílias exponenciais
Se X1, X2, ..., Xn é uma amostra aleatória simples de uma distribuição exponencial com parâmetro θ, ou seja,
f(x|θ) = θe-θx, θ > 0,
então, o estimador de θ pelo método dos momentos é
