Questões de Concurso
Filtrar
83 Questões de concurso encontradas
Página 5 de 17
Questões por página:
Questões por página:
Concurso:
IFB
Disciplina:
Engenharia Eletrônica
mostrar texto associado
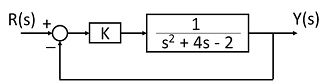
Quais valores de K tornam o sistema estável?
Concurso:
IFB
Disciplina:
Engenharia Eletrônica
mostrar texto associado
Determine a função de transferência Y(s)/R(s) do sistema.
Concurso:
SEAD-AP
Disciplina:
Engenharia Eletrônica
Considere uma sequência discreta e causal x(n), definida apenas para n≥0. Aplicando-se a Transformada Z nesta sequência obtém-se :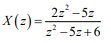
Os valores das três primeiras amostras da sequência x(n), ou seja, 
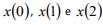, respectivamente, são:
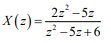Os valores das três primeiras amostras da sequência x(n), ou seja, 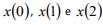, respectivamente, são:
Concurso:
SEAD-AP
Disciplina:
Engenharia Eletrônica
Um servossistema contínuo, linear e invariante no tempo, modelado em espaço de estados, tendo X(t) como vetor de estados, apresenta sua dinâmica ditada pelas equações a seguir, em que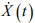 
é a derivada do vetor de estados, y(t) é a saída e u(t) é a entrada.
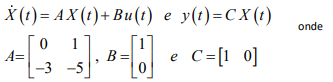
Utilizando-se uma realimentação de Estados com a lei de controle dada por: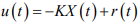
, em que K é o vetor de ganhos e r(t) é uma entrada de referência, pretende-se alocar seus dois polos de malha fechada nas posições reais 
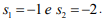Para obter esse resultado, o valor do vetor de ganhos K é:
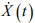é a derivada do vetor de estados, y(t) é a saída e u(t) é a entrada.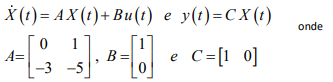 Utilizando-se uma realimentação de Estados com a lei de controle dada por:
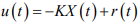, em que K é o vetor de ganhos e r(t) é uma entrada de referência, pretende-se alocar seus dois polos de malha fechada nas posições reais 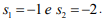Para obter esse resultado, o valor do vetor de ganhos K é:
Concurso:
SEAD-AP
Disciplina:
Engenharia Eletrônica
Considere uma planta, de modelo contínuo e linear, tendo como entrada o sinal u(t) e como saída o sinal y(t) e sua Função de Transferência, em Laplace, é dada por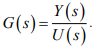 
O gráfico da figura a seguir mostra o traçado do Lugar das Raízes para esta planta sujeita a uma realimentação de saída com lei de controle: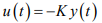
e o ganho K varia de zero a infinito.
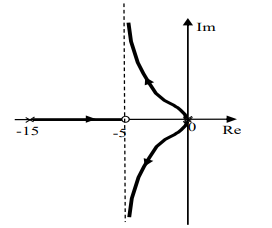
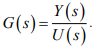
O gráfico da figura a seguir mostra o traçado do Lugar das Raízes para esta planta sujeita a uma realimentação de saída com lei de controle:
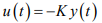e o ganho K varia de zero a infinito. 