Filtrar
15 Questões de concurso encontradas
Página 1 de 3
Questões por página:
Tais afirmativas enquadram-se no contexto da teoria dos jogos, que é aplicável quando as empresas atuam em uma estrutura de mercado, definida como um(a)
A teoria dos mercados eficientes é a aplicação da teoria de expectativas racionais à determinação de preços dos títulos nos mercados financeiros. Segundo essa teoria, os preços vigentes dos títulos refletirão todas as informações disponíveis, de forma que todas as oportunidades inexploradas de lucros sejam eliminadas.
Na hipótese de mercados eficientes,
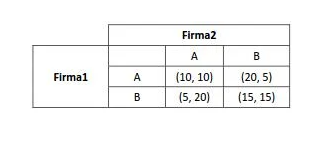
O primeiro número dentro de cada parêntese é o lucro da firma 1 e o segundo, o da firma 2.
Um equilíbrio do jogo é dado por {X, Y}, sendo X a estratégia da firma 1 (A ou B) e Y a da firma 2 (A ou B).
Os equilíbrios cooperativo e de Nash em estratégias puras são, respectivamente,
Suponha que duas pessoas joguem o seguinte jogo: ambos devem escolher simultaneamente um número real (x e R), que satisfaça duas condições:
x ≥ 0 e x ≤ 100.
Se o número escolhido por um dos jogadores for igual à metade da média entre os dois números escolhidos por ambos, esse jogador ganha o jogo.
Assuma que o par (x1, x2) representa os números escolhidos pelos jogadores 1 e 2, respectivamente.
Logo, o equilíbrio de Nash será dado por
Em relação a tais desafios, assinale (V) para a afirmativa verdadeira e (F) para a falsa.
( ) A alta da taxa de inflação de 2010 poderia impactar a taxa de 2011. ( ) Conciliar o regime de metas com um crescimento mais elevado do PIB. ( ) Reduzir a meta inflacionária para o nível de países desenvolvidos, abaixo de 1%.
As afirmativas são, respectivamente,