Questões de Concurso

A matriz abaixo mostra um jogo na sua forma estratégica. A e B são os jogadores participantes e suas estratégias são, respectivamente, 1 e 2 para A, e I, II e III para B. Dentro de cada célula da matriz o número à esquerda é o ganho de A, e o número à direita, o ganho de B. Os jogadores decidem suas estratégias simultaneamente, têm conhecimento das estratégias próprias e do adversário, e também dos ganhos de ambos em cada célula.

Pode-se, então, afirmar que

Duas empresas A e B são grandes concorrentes no mercado de um determinado bem X. Em uma determinada semana, as duas empresas devem escolher entre duas estratégias para vender seus produtos no supermercado C: manter o preço da semana anterior ou dar desconto em relação a esse preço. A matriz de payoffs das duas empresas para as quatro combinações de estratégias possíveis está reproduzida abaixo:

É correto concluir que, nesse mercado,

A matriz abaixo representa um jogo de decisões simultâneas entre duas pessoas, I e II. Em cada célula da matriz aparece, à esquerda, o retorno de I e, à direita, o de II. As estratégias de I e de II são, respectivamente, S₁, S₂ e S₃ e Q₁, Q₂ e Q₃.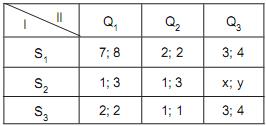



Suponha que os dois jogadores conheçam, antecipadamente, todas as estratégias e retornos envolvidos. Para que a combinação de estratégias S₂Q₃ seja um equilíbrio de Nash, é suficiente que

A matriz abaixo representa um jogo com decisões simultâneas de duas pessoas, A e B. Em cada célula da matriz, o valor à esquerda é o retorno monetário de A, e o valor à direita é o de B. Há células não preenchidas ou com incógnitas X, Y, Z e W. Ambos os participantes têm conhecimento de todos os valores nas células e de todas as estratégias possíveis: I a III, para A e 1 a 3, para B.



O exame da matriz leva à conclusão de que