Questões de Concurso

Um engenheiro está projetando uma nova roda-gigante para um parque de diversões. Ele precisa determinar a altura máxima que a roda-gigante atingirá durante uma volta completa, levando em consideração a função trigonométrica que descreve o movimento da cabine ao longo do tempo.
O engenheiro modelou o movimento vertical da cabine da roda-gigante com a função trigonométrica h(t) = A ∙ sen(Bt) +C onde t representa o tempo em segundos, h(t) é a altura em metros, e A, B e C são constantes.
Considerado a função h(t) = 30sen(π/15 t) + 40, a altura máxima que a cabine da roda-gigante atingirá durante uma volta completa é

Considere um retângulo ABCD cujo lado menor mede L e o lado maior mede o dobro do lado menor. A razão entre a área do retângulo e a diagonal D é:

Considere a função real f(x), definida como sendo o determinante da matriz A, dada a seguir:

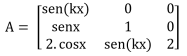
Se o período da função f é 6π, o valor positivo de k e o conjunto imagem da função f são, respectivamente, iguais a:

A sucessão numérica (1,1,2,3,5,8,13, ...) mostra os sete primeiros termos da Sequência de Fibonacci. Nela, cada termo, a partir do terceiro, é igual a soma dos dois termos imediatamente anteriores a ele. Essa sequência possui muitas propriedades interessantes, e uma delas, descoberta por Charles Raine, está relacionada aos triângulos pitagóricos, ou seja, a um triângulo retângulo cujos três lados são números inteiros. Tomando-se quatro termos consecutivos dessa sequência, o produto dos termos extremos e o dobro do produto dos termos centrais são catetos de um triângulo pitagórico.
Logo, tomando-se o 5º,6º,7º e 8º termos da sequência de Fibonacci, pode-se obter os catetos de um triângulo retângulo cujo produto da altura relativa à hipotenusa pela própria hipotenusa é igual a:

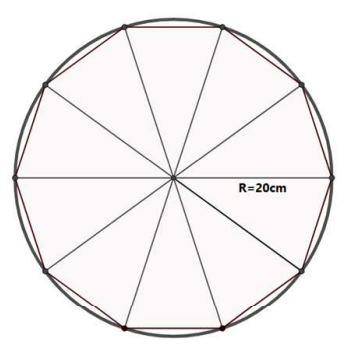
Uma pizza G, com a forma de uma circunferência de raio 20 cm, foi dividida em 10 fatias iguais. Todas estas fatias tem o formato próximo ao de triângulos isósceles, cujos lados iguais correspondem ao raio da pizza, conforme a ilustração abaixo. Determine a medida do lado da base desses triângulos.