Considere uma economia que seja descrita pelo sistema de equações apresentado a seguir.
Função de produção: Y = F(K, L)
FK > 0, FL > 0, FKL > 0, FLL<0, FKK < 0, em que Fi é a primeira derivada da função de produção com relação ao insumo i e Fii é a segunda derivada da função de produção com relação ao insumo i.
Função demanda de trabalho: 
Função investimento: 
I´ I´ é a derivada do investimento em relação à taxa de juros.
Função consumo: C = C(Y - T); 0 C´ C´é a derivada do consumo em relação à renda disponível.
Equação de consistência macroeconômica: Y = C + I + G + dK
Equilíbrio monetário: 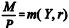 em que Y é o produto, L é a
em que Y é o produto, L é a
quantidade de trabalho, K é o estoque de capital, w é o salário nominal, P é o nível geral de preços, I é o investimento, Q é o Q de Tobin, r é a taxa nominal de juros, p é a taxa de inflação, C é o consumo, T é a tributação autônoma, G corresponde aos gastos autônomos do governo, m é a função demanda por moeda, M é o estoque de moeda, d é a depreciação do estoque de capital.
Considerando que, na economia acima descrita, vija um regime no qual o governo controla a quantidade de moeda e que o estoque de capital seja constante ao longo do tempo, julgue o item seguinte.
O aumento da quantidade de moeda desloca para a direita a curva de equilíbrio monetário, o que proporciona redução da taxa de juros, aumento do produto e do emprego e redução do salário real.


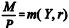 em que Y é o produto, L é a
em que Y é o produto, L é a