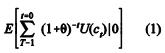Considere que, em um modelo CAPM, o consumidor tenha um horizonte de tempo T e pretenda maximizar a função utilidade esperada apresentada a seguir:
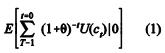
Em que: E(.| t) é a expectativa condicional, dadas as informações disponíveis no instante t; θ é a taxa de preferência intertemporal.
Considere, ainda, que, no instante t, o consumidor decida alocar sua riqueza em qualquer dos n ativos arriscados existentes na economia, cujo retorno (líquido) estocástico é dado por z it, com i = 1, ..., n, e que exista um ativo livre de risco com retorno rt .
Considere, por fim, que as condições de primeira ordem para o problema do consumidor sejam descritas por
U´(c t = (1 + θ) -1 E [ U´(ct+1) (1 + zit ) | t ] i = 1, ..., n (2)
U´(c t ) = (1 + θ) -1 (1 + rt ) E[U´(ct+1) | t] (3)
Com base nesse conjunto de informações, julgue o item seguinte.
Quanto maior for a covariância do ativo com a utilidade do consumo do agente, menor será o retorno esperado do ativo.