Concurso:
Instituto Federal Pará
Disciplina:
Estatística
O modelo de um experimento fatorial com dois fatores num delineamento inteiramente casualizado com n repetições podeser escrito como:
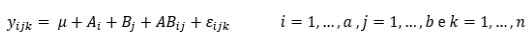
em que:
• yijk é a resposta da k-ésima repetição do i-ésimo nível do fator A e j-ésimo nível do fator B; • μ é uma constante comum a todas as observações; • Ai é o efeito do i-ésimo nível do fator A; • Bj é o efeito da j-ésimo nível do fator B; • ABij é o efeito da interação entre o i-ésimo nível do fator A e j-ésimo nível do fator B; e, • ξijk é o erro associado à resposta yijk, de modo que ξijk ~ N(0; σ2).
Ao construir uma tabela de análise de variância para que seja feita a inferência no modelo, o número de graus de liberdadeassociado à soma de quadrados da interação é:
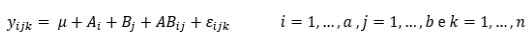
em que:
• yijk é a resposta da k-ésima repetição do i-ésimo nível do fator A e j-ésimo nível do fator B; • μ é uma constante comum a todas as observações; • Ai é o efeito do i-ésimo nível do fator A; • Bj é o efeito da j-ésimo nível do fator B; • ABij é o efeito da interação entre o i-ésimo nível do fator A e j-ésimo nível do fator B; e, • ξijk é o erro associado à resposta yijk, de modo que ξijk ~ N(0; σ2).
Ao construir uma tabela de análise de variância para que seja feita a inferência no modelo, o número de graus de liberdadeassociado à soma de quadrados da interação é: