O sistema da figura abaixo representa uma máquina de massa total M, com uma parte girante, de massa m e excentricidade e, conforme figura. A coordenada x varia com o tempo e localiza a parte não girante da máquina. A máquina é suportada por uma suspensão de constante elástica k e constante de amortecimento c. A equação diferencial do movimento é Mx + cx + kx = mep2 cos(pt) . O bloco não girante terá um movimento harmônico persistente expresso por x(t) = Xcos(pt − Ψ) , onde X é a amplitude da vibração e Ψ é a diferença de fase. Sobre tal sistema considere:
I. A amplitude da vibração, X, aumenta proporcionalmente ao valor da velocidade angular p.
II. A amplitude da vibração, X, depende do fator de ampliação que por sua vez depende da razão entre a velocidade angular, p, e a frequência natural do sistema, ω.
III. O fator de ampliação não depende do índice de amortecimento.
IV. Haverá ressonância quando não houver amortecimento e a velocidade angular for igual à frequência natural. 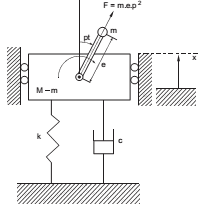
Está correto o que consta em