Concurso:
TRE-MG
Disciplina:
Estatística
O modelo de componentes principais é utilizado para representar a estrutura de variância-covariância em função de um número reduzido de combinações lineares das variáveis originais, com o objetivo de se ter uma redução de dados e uma melhor interpretação destes. Para o vetor aleatório 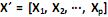 com matriz de covariância S e autovalores iguais a
com matriz de covariância S e autovalores iguais a 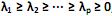 , e as combinações lineares:
, e as combinações lineares:
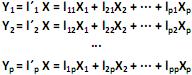
O modelo de componentes principais corresponde às combinações lineares não correlacionadas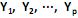 com vetores de coeficientes
com vetores de coeficientes 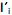 de comprimento unitário, que apresentam as maiores variâncias Var
de comprimento unitário, que apresentam as maiores variâncias Var 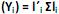 . Diante do exposto, é correto afirmar que
. Diante do exposto, é correto afirmar que
I. o primeiro componente principal é a combinação linear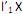 que maximiza Var
que maximiza Var 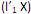 sujeito a
sujeito a 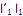 = 1.
= 1.
II. o i-ésimo componente principal é a combinação linear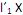 que maximiza Var
que maximiza Var 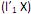 = 1 e Cov (
= 1 e Cov (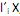 ,
, 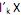 ) = 0, para k < i.
) = 0, para k < i.
III. sendo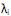 os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por
os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por 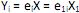 +
+  , onde i = 1, ··· p.
, onde i = 1, ··· p.
IV. Var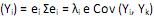 = 0, para i = 1,2, ···, p e i ≠ k.
= 0, para i = 1,2, ···, p e i ≠ k.
V. a proporção da variância total devido ao k-ésimo componente principal é dada por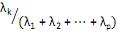 para k = 1, ···, p.
para k = 1, ···, p.
Estão corretas apenas as afirmativas
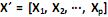 com matriz de covariância S e autovalores iguais a
com matriz de covariância S e autovalores iguais a 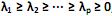 , e as combinações lineares:
, e as combinações lineares: 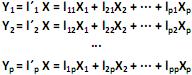
O modelo de componentes principais corresponde às combinações lineares não correlacionadas
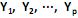 com vetores de coeficientes
com vetores de coeficientes 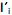 de comprimento unitário, que apresentam as maiores variâncias Var
de comprimento unitário, que apresentam as maiores variâncias Var 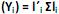 . Diante do exposto, é correto afirmar que
. Diante do exposto, é correto afirmar que I. o primeiro componente principal é a combinação linear
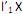 que maximiza Var
que maximiza Var 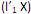 sujeito a
sujeito a 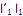 = 1.
= 1. II. o i-ésimo componente principal é a combinação linear
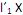 que maximiza Var
que maximiza Var 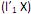 = 1 e Cov (
= 1 e Cov (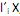 ,
, 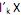 ) = 0, para k < i.
) = 0, para k < i. III. sendo
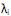 os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por
os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por 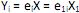 +
+  , onde i = 1, ··· p.
, onde i = 1, ··· p. IV. Var
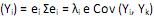 = 0, para i = 1,2, ···, p e i ≠ k.
= 0, para i = 1,2, ···, p e i ≠ k. V. a proporção da variância total devido ao k-ésimo componente principal é dada por
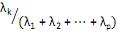 para k = 1, ···, p.
para k = 1, ···, p. Estão corretas apenas as afirmativas