O modelo de análise fatorial representa a estrutura de covariância entre muitas variáveis aleatórias 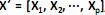, através de poucas variáveis não observáveis F´ = [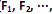 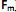] também conhecidas como fatores, construtos ou fatores comuns. Sendo E(X) = µ e V(X) = S, o modelo fatorial é expresso por X – µ = LF + e. A matriz 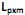é conhecida como matriz das cargas fatoriais e seus elementos, 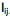, carga da variável i no fator j e as variáveis aleatórias F e em + p são não observáveis. Analise as afirmativas, marque V para as verdadeiras e F para as falsas.

( ) No modelo fatorial ortogonal, as variáveis não observáveis F e e são independentes, E(F) = 0, V(F) = E(F´F) = I, E(e) = 0, V(e) = E(e´e) = ψ. A matriz ψ é não diagonal, V(X) = S = L´L + ψ e Cov (X, F) = L.
( ) Um método de estimação para as cargas do modelo fatorial ortogonal é através de componentes principais, onde se utiliza a decomposição espectral da matriz S.
( ) Para se utilizar o método de máxima verossimilhança para estimar as cargas, é acrescida a suposição de que F e e têm distribuição normal multivariada. As comunalidades (elementos da diagonal LL´) têm como estimadores a proporção da variância total estimada pelo particular fator.
( ) Para melhorar a explicação do modelo fatorial, sem alterar a ortogonalidade dos fatores, muitas vezes, usa-se uma transformação ortogonal das cargas fatoriais, que, consequentemente, transforma os fatores. Esse procedimento é conhecido como rotação fatorial.
( ) Dependendo da natureza dos dados, os fatores não precisam ser ortogonais. Assim, para melhorar a explicação do modelo fatorial, pode-se utilizar a rotação oblíqua, onde cada variável é expressa em termos de um número máximo de fatores.
A sequência está correta em