Uma variável aleatória Gama é definida para valores reais e positivos e sua função densidade é dada por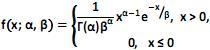

com parâmetros α > 0 e ß > 0.

Diante do exposto, analise as afirmativas.
I. Pode-se demonstrar que E(x) = αß e Var(x) = αalpha;ß².

II. A função gama é dada por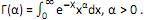

III. Pode-se mostrar que G(α) = (α – 1) G(α – 1) e para α inteiro, G(α) = (α – 1)!.

IV. Quando α = 1, a função densidade da gama e igual à distribuição exponencial com parâmetro ß.

V. Quando α = v/2 e ß = 2, com v > 0 inteiro, a função densidade da gama é igual à distribuição Qui-quadrado com v graus de liberdade.

Estão corretas apenas as afirmativas