Questões de Concurso
Filtrar
2.950 Questões de concurso encontradas
Página 36 de 590
Questões por página:
Questões por página:
Disciplina:
Matemática
O método de integração tem sua origem no método da exaustão, o qual admite que uma grandeza possa ser subdividida indefinidamente e sua base seja a proposição: se de uma grandeza qualquer subtrai-se uma parte não menor que sua metade, do restante subtrai-se também uma parte não menor que sua metade, e assim por diante, se chegará, por fim, a uma grandeza menor que qualquer outra predeterminada da mesma espécie. Arquimedes aplicou este método para calcular a área de uma região limitada por um arco de parábola e pelo segmento que une as extremidades de tal arco (problema conhecido como a quadratura da parábola). Considere o arco de parábola 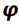 de extremidades
de extremidades
A e B e os pontos C, D, E de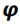 , obtidos traçandose os segmentos LC, MD, NE paralelos ao eixo focal da parábola, onde L, M, N são pontos médios dos segmentos AB, AC, BC, respectivamente (veja Figura 1). Denotando, de maneira geral,
, obtidos traçandose os segmentos LC, MD, NE paralelos ao eixo focal da parábola, onde L, M, N são pontos médios dos segmentos AB, AC, BC, respectivamente (veja Figura 1). Denotando, de maneira geral, 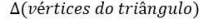 como área do triangulo de vértices destacados, Arquimedes mostrou que
como área do triangulo de vértices destacados, Arquimedes mostrou que
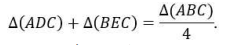 Repetindo sucessivamente esse raciocínio, conclui-se que a área da região limitada pelo arco de parábola e pelo segmento AB (segmento parabólico) é dada por
Repetindo sucessivamente esse raciocínio, conclui-se que a área da região limitada pelo arco de parábola e pelo segmento AB (segmento parabólico) é dada por
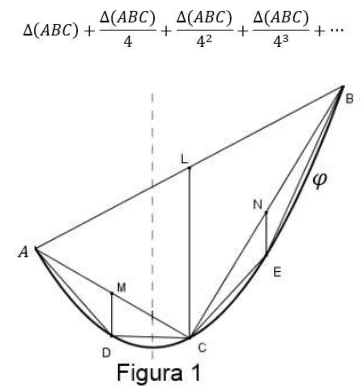
Dada a parábola y = x2 - 4x + 4 e seus pontos A(1,1) e B(4,4), o valor da área do segmento parabólico, em unidade de área, é:
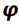 de extremidades
de extremidades A e B e os pontos C, D, E de
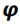 , obtidos traçandose os segmentos LC, MD, NE paralelos ao eixo focal da parábola, onde L, M, N são pontos médios dos segmentos AB, AC, BC, respectivamente (veja Figura 1). Denotando, de maneira geral,
, obtidos traçandose os segmentos LC, MD, NE paralelos ao eixo focal da parábola, onde L, M, N são pontos médios dos segmentos AB, AC, BC, respectivamente (veja Figura 1). Denotando, de maneira geral, 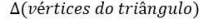 como área do triangulo de vértices destacados, Arquimedes mostrou que
como área do triangulo de vértices destacados, Arquimedes mostrou que 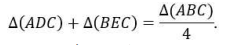 Repetindo sucessivamente esse raciocínio, conclui-se que a área da região limitada pelo arco de parábola e pelo segmento AB (segmento parabólico) é dada por
Repetindo sucessivamente esse raciocínio, conclui-se que a área da região limitada pelo arco de parábola e pelo segmento AB (segmento parabólico) é dada por 
Dada a parábola y = x2 - 4x + 4 e seus pontos A(1,1) e B(4,4), o valor da área do segmento parabólico, em unidade de área, é:
Disciplina:
Matemática Financeira
João foi a uma concessionária comprar um carro novo. O modelo que ele escolheu custa R$ 78.750,00. O vendedor, Paulo, lhe apresentou duas opções de compras parceladas, ambas com 24 prestações fixas a serem pagas a partir do mês seguinte ao da compra.
Proposta I: sem entrada e com taxa de juros compostos de 2% ao mês.
Proposta II: com uma entrada de R$ 18.750,00 e com taxa de juros compostos de 1,8% ao mês. João, então, foi para casa calcular os valores totais nas duas propostas apresentadas por Paulo.
Usando 1,0224 = 1,6 e 1,01824 = 1,5 calcule a diferença aproximada dos valores totais a serem pagos nas duas propostas apresentadas por Paulo.
Proposta I: sem entrada e com taxa de juros compostos de 2% ao mês.
Proposta II: com uma entrada de R$ 18.750,00 e com taxa de juros compostos de 1,8% ao mês. João, então, foi para casa calcular os valores totais nas duas propostas apresentadas por Paulo.
Usando 1,0224 = 1,6 e 1,01824 = 1,5 calcule a diferença aproximada dos valores totais a serem pagos nas duas propostas apresentadas por Paulo.
Disciplina:
Matemática
Uma fossa séptica é considerada uma pequena unidade de tratamento de esgoto doméstico, uma opção para residências onde ainda não existe saneamento básico. Nela, o esgoto passa por três etapas: na 1ª etapa, é encaminhado para um tanque impermeável, a fossa séptica em si, onde a matéria orgânica é depositada no fundo, formando um lodo que passará por um processo de degradação; na 2ª etapa, o líquido presente na fossa séptica irá passar por um filtro anaeróbico e, na 3ª etapa, será depositado no sumidouro, onde irá escoar o material, pois não possui fundo.
A imagem abaixo é de um projeto de fossa séptica, em formato de paralelepípedo de base quadrada ligada a um filtro anaeróbico cilíndrico, e este a um sumidouro também em formato cilíndrico.
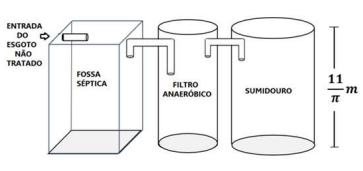
No projeto, ficou estabelecido que os três têm a mesma altura de 11/π metros, e que a base da fosse séptica tem lado 2m. Sabe-se que o volume do filtro anaeróbio é a metade do volume da fossa séptica, e que o volume do sumidouro é o dobro do volume da fosse séptica. Sendo assim, determine a razão entre o raio da base do sumidouro e o raio da base do filtro anaeróbio.
A imagem abaixo é de um projeto de fossa séptica, em formato de paralelepípedo de base quadrada ligada a um filtro anaeróbico cilíndrico, e este a um sumidouro também em formato cilíndrico.

No projeto, ficou estabelecido que os três têm a mesma altura de 11/π metros, e que a base da fosse séptica tem lado 2m. Sabe-se que o volume do filtro anaeróbio é a metade do volume da fossa séptica, e que o volume do sumidouro é o dobro do volume da fosse séptica. Sendo assim, determine a razão entre o raio da base do sumidouro e o raio da base do filtro anaeróbio.
Disciplina:
Matemática
O ITBI, Imposto Sobre Transmissão de Bens Imóveis, é um tributo municipal cobrado sempre que ocorre uma compra ou transferência de imóveis. Ele tem como fato gerador a transmissão entre pessoas vivas de propriedade ou domínio útil de bens imóveis, e tem como base de cálculo o valor venal do bem. Em Teresina-PI, atualmente a alíquota é de 3% para vendas de imóveis em áreas residenciais.
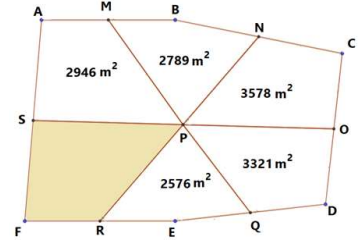
Seja um terreno, em Teresina-PI, que foi loteado em seis partes, conforme a figura acima, onde os pontos M, N, O, Q, R, S são os pontos médios dos lados AB, BC, CD, DE, EF e FA, respectivamente, e o ponto P a interseção comum dos segmentos MQ, NR e OS.
Na figura, temos ainda as áreas de cinco desses terrenos, determinados por quadriláteros. São elas:
(PSAM) = 2946m2, (PMBN) = 2789m2, (PNCO) = 3578m2, (PODQ) = 3321m2, (PQER) = 2576m2 .
Calcule o ITBI a ser pago pelo comprador do terreno, determinado pelo quadrilátero PRFS, sabendo que o metro quadrado desse terreno custou R$ 100,00.

Seja um terreno, em Teresina-PI, que foi loteado em seis partes, conforme a figura acima, onde os pontos M, N, O, Q, R, S são os pontos médios dos lados AB, BC, CD, DE, EF e FA, respectivamente, e o ponto P a interseção comum dos segmentos MQ, NR e OS.
Na figura, temos ainda as áreas de cinco desses terrenos, determinados por quadriláteros. São elas:
(PSAM) = 2946m2, (PMBN) = 2789m2, (PNCO) = 3578m2, (PODQ) = 3321m2, (PQER) = 2576m2 .
Calcule o ITBI a ser pago pelo comprador do terreno, determinado pelo quadrilátero PRFS, sabendo que o metro quadrado desse terreno custou R$ 100,00.
Disciplina:
Matemática
Uma pizza G, com a forma de uma circunferência de raio 20 cm, foi dividida em 10 fatias iguais. Todas estas fatias tem o formato próximo ao de triângulos isósceles, cujos lados iguais correspondem ao raio da pizza, conforme a ilustração abaixo. Determine a medida do lado da base desses triângulos.