Questões de Concurso
Filtrar
220 Questões de concurso encontradas
Página 10 de 44
Questões por página:
Uma amostra aleatória simples X1, X2, ..., X16 será retirada de uma população normal com média µ e desvio-padrão σ, ambos desconhecidos. Para estimá-los, são propostas as estatísticas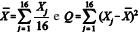 
. Com base nessas informações, julgue o item seguinte.
A matriz de covariância do vetor aleatório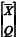 
é a matriz de informação de Fisher.
Uma amostra aleatória simples X1, X2, ..., X16 será retirada de uma população normal com média µ e desvio-padrão σ, ambos desconhecidos. Para estimá-los, são propostas as estatísticas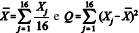 
. Com base nessas informações, julgue o item seguinte.
Para a estimação da média populacional µ, a média amostral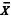 
é um estimador não tendencioso de mínima variância. Qualquer outro estimador não tendencioso para a estimação de µ, como, por exemplo, a mediana amostral, terá um desvio-padrão uniformemente maior que 0,25σ.
As medidas de concordância de Yule e de Goodman e Kruskal — com a hipótese de que, em razão da campanha proposta pela instituição, a probabilidade de um operário sofrer algum tipo de acidente diminui — são superiores a -0,2 e inferiores a 0,2.
Considerando-se a tabela de contingência 2 × 2 que cruza o grupo (caso/controle) com o número de operários (não sofreram/sofreram algum tipo de acidentes), é possível se obter uma medida de associação chamada coeficiente kappa, cujo valor é inferior a !0,02 ou superior a 0,02.
Considere-se que a ocorrência de acidentes segue uma distribuição de Poisson e a hipótese nula (H0) do teste é: “a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, mas se um operário for exposto à campanha, a probabilidade de ele, operário, sofrer algum tipo de acidente é reduzida para 0,02”. A hipótese alternativa (Ha) é: “a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, independentemente de o operário ter sido ou não exposto à campanha”. Nessa situação, se a estatística qui-quadrado sob H0 for igual a Q0 e se a estatística qui-quadrado sob Ha for igual a Qa, então é correto afirmar que a razão Q0/Qa é a estatística de razão de verossimilhança para o teste em questão.
