Questões de Concurso

Deseja-se testar, a um determinado nível de significância, a hipótese de igualdade das médias das notas de uma matéria numa escola para K (K > 2) grupos de alunos. Cada grupo foi submetido a um esquema de aula diferente dos demais. Para a tomada de decisão, pensa-se em utilizar o teste de Kruskal-Wallis. É correto afirmar que este teste NÃO se aplica

Uma amostra aleatória com 16 elementos é extraída de uma população normal de tamanho infinito com média µ e desvio padrão desconhecido. O valor da média amostral e o valor da variância amostral foram iguais a M e 625, respectivamente. Deseja-se testar a hipótese H₀: µ = 90 (hipótese nula) contra H₁: µ > 90 (hipótese alternativa) com base nos resultados apresentados pela amostra, ao nível de significância de 5%. Utilizou-se para o teste a distribuição t de Student, considerando t_0,05 o quantil da distribuição t de Student para o teste unicaudal tal que P (t > t_0,05) = 5%.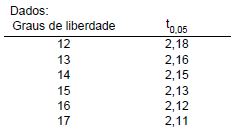



Sabendo-se que H₀ não foi rejeitada, então o valor de M foi, no máximo,

Os salários de todos os 170 empregados de uma empresa apresentam uma distribuição normal com um desvio padrão igual a R$ 364,00. Uma pesquisa com 49 empregados, selecionados ao acaso, detectou uma média de R$ 1.560,00 para os salários desta amostra. Com base no resultado desta amostra e considerando que, na distribuição normal padrão (Z), a probabilidade P(Z > 2,05) = 2%, obtém-se que o intervalo de confiança de 96% para a média dos salários da empresa, em R$, é igual a

Um estudo realizado em uma fábrica determinou que o intervalo de confiança de 90% para a vida média dos equipamentos, em horas, foi [891,80; 908,20]. Para esta conclusão, considerou-se a população normalmente distribuída, de tamanho infinito e uma amostra aleatória de 64 equipamentos. Se, na distribuição normal padrão (Z), a probabilidade P(Z > 1,64) = 5%, então, o desvio padrão populacional, em horas, desta população é igual a

Considere uma amostra de 8 elementos proveniente de uma população com função densidade  Com base nesta amostra, apurou-se que o estimador de máxima verossimilhança da variância da população foi igual a 3. O maior valor apresentado nesta amostra foi