Em um estudo estatístico, uma amostra aleatória simples X₁, X₂, …, X_n, foi retirada de uma população cuja função de distribuição de probabilidade é P(X = k) =Ce^-θk, em que C representa o fator de normalização, e é o número de Neper (ou de Euler), θ > 0 denota o parâmetro da distribuição e k =0, 1, 2, … . Acerca dessas informações, e considerando que seja a média amostral, julgue o próximo item.

De acordo com a lei fraca dos grandes números, à medida que o tamanho da amostra aumenta, a variável aleatória converge para uma distribuição normal padrão.

Em um estudo estatístico, uma amostra aleatória simples X₁, X₂, …, X_n, foi retirada de uma população cuja função de distribuição de probabilidade é P(X = k) =Ce^-θk, em que C representa o fator de normalização, e é o número de Neper (ou de Euler), θ > 0 denota o parâmetro da distribuição e k =0, 1, 2, … . Acerca dessas informações, e considerando que seja a média amostral, julgue o próximo item.

A estatística é um estimador de momentos do parâmetro θ.

Um estudo mostrou que a distribuição das rendas de determinada população de trabalhadores segue uma variável aleatória X cuja função de probabilidade acumulada é expressa por . Com base nessas informações, julgue o seguinte item.

A média da distribuição X é superior a 3, e a sua variância é inferior a 10.

Um estudo mostrou que a distribuição das rendas de determinada população de trabalhadores segue uma variável aleatória X cuja função de probabilidade acumulada é expressa por 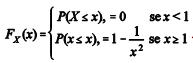. Com base nessas informações, julgue o seguinte item.

A variável aleatória X é contínua, e P(X = 0) = P(X = 2) = P(X = 5) = P(X = 10) = 0.

Um estudo mostrou que a distribuição das rendas de determinada população de trabalhadores segue uma variável aleatória X cuja função de probabilidade acumulada é expressa por . Com base nessas informações, julgue o seguinte item.

A moda e a mediana dessa distribuição de rendas são, respectivamente, iguais a 1 e 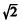.