Questões do concurso:
SEFAZ-RJ - 2013
limpar filtros
200 Questões de concurso encontradas
Página 11 de 40
Questões por página:
Questões por página:
Concurso:
SEFAZ-RJ
Disciplina:
Raciocínio Lógico
Em um clube com 440 associados ocorre uma eleição para presidente, em que os dois primeiros colocados, entre 6 candidatos, passam para um segundo turno. Se, no primeiro turno, todos os 440 associados votam, cada um, em apenas um dos candidatos, então o número mínimo de votos que assegura a um determinado candidato a sua participação no segundo turno é:
Concurso:
SEFAZ-RJ
Disciplina:
Raciocínio Lógico
A seguinte sequência numérica obedece, a partir do segundo número, a uma determinada lei de formação.
6, 42, 114, 222, 366, ....
O sexto termo dessa sequência é :
6, 42, 114, 222, 366, ....
O sexto termo dessa sequência é :
Concurso:
SEFAZ-RJ
Disciplina:
Estatística
Seja p a probabilidade de ocorrer cara quando se lança uma determinada moeda. Com base em 100 lançamentos da moeda, deseja-se testar a hipótese de que a moeda é não viciada (p = 0,5) contra a alternativa de que p = 0,8. Com base na variável aleatória p que representa a proporção de caras em 100 lançamentos, estabeleceu-se para o teste a seguinte região crítica (RC): RC = { p ≥0,75}.Sendo β a probabilidade do erro do tipo II, e admitindo-se a aproximação à normal para a distribuição de p, o valor de β é:
Concurso:
SEFAZ-RJ
Disciplina:
Estatística
Uma população infinita tem desvio padrão igual a 10 e média μ desconhecida. Uma amostra aleatória com reposição de tamanho n foi selecionada dessa população. Sabe-se que:
I. O valor de n deve ser tal que, com probabilidade 16%, o erro em se estimar μ seja superior a 1.
II. Se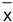 
é o valor da média amostral da amostra selecionada, então 
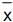= 40,7
Baseado na amostra de tamanho n e nas condições I e II acima, um intervalo de confiança para µ com coeficiente de confiança de 95% é dado por :
Concurso:
SEFAZ-RJ
Disciplina:
Estatística
Se Z tem distribuição normal padrão, então:
P(Z < 0,8) = 0,788; P(Z < 1,25) = 0,894; P(Z < 1,4) = 0,9
P(Z < 1,64) = 0,95; P(Z < 1,96) = 0,975; P(Z < 2) = 0,977
O tempo necessário para o atendimento de uma pessoa em um guichê de uma repartição pública tem distribuição normal com média μ = 140 segundos e desvio padrão σ = 50 segundos. A probabilidade de que um indivíduo, aleatoriamente selecionado, espere entre 3 e 4 minutos para ser atendido é:
P(Z < 0,8) = 0,788; P(Z < 1,25) = 0,894; P(Z < 1,4) = 0,9
P(Z < 1,64) = 0,95; P(Z < 1,96) = 0,975; P(Z < 2) = 0,977
O tempo necessário para o atendimento de uma pessoa em um guichê de uma repartição pública tem distribuição normal com média μ = 140 segundos e desvio padrão σ = 50 segundos. A probabilidade de que um indivíduo, aleatoriamente selecionado, espere entre 3 e 4 minutos para ser atendido é:
