Devido ao crescimento no número de ocorrências violentas em determinado bairro decidiu-se instalar um posto policial cuja localização foi escolhida, por razões estratégicas, tomando-se como referência três regiões − R₁, R₂, R₃ − de maior incidência de eventos dessa natureza. Se R₁, R₂, R₃ forem representadas no plano cartesiano por (6,1), (6,9) e (13,1), respectivamente, então o posto deverá ser representado por um ponto P, o mais próximo possível de R₁ e R₂, equidistante destes e, além disso, a uma distância de 5u.c. de R₃.

Assim sendo, a medida da distância do ponto P a R₂, em unidades de comprimento, deverá ser, aproximadamente, igual a

Sabe-se que a capacidade de uma taça na forma de um cone equilátero é de 72√3π cm³ .

Se uma pessoa colocou um líquido nessa taça até a altura correspondente a 2/3 do raio máximo da taça, então sobre o volume de líquido nela colocado, em cm³, pode-se afirmar:

Os pontos A, B, C e D representam, no plano complexo, os vértices de uma mesa de sinuca, retangular, de lados paralelos aos eixos coordenados e cujo centro O coincide com a origem do referido sistema de coordenadas. Após uma tacada na direção de z = 1 + i, uma bola colocada no ponto P segue até Q, na lateral dessa mesa, indo, em seguida, até R.

Sabendo-se que a bola se desvia com o mesmo ângulo com que incide e que os pontos A e P são afixos dos números complexos z₁ = 3 + 2i e z₂ = − 1/2, respectivamente, pode-se afirmar que o ponto R é afixo de um número complexo cujo argumento principal θ é tal que

Considere uma circunferência de centro C e raio 4cm, que se apoia sobre uma reta tangente r, como indicado na figura, e P, um ponto da circunferência posicionado na horizontal à direita de C.



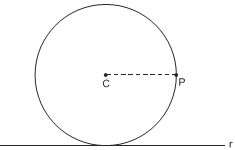
Sabe-se que P se desloca sobre a circunferência, no sentido horário, até ocupar uma posição em que sua distância à reta r mede 3cm.

Se a mesma localização de P fosse obtida através de um deslocamento no sentido anti-horário, então é correto afirmar que a amplitude da rotação feita por P mediria, em radianos,

Devido a um problema na emissão digital de senhas, um funcionário recebeu uma caixa contendo cartões numerados para serem distribuídos ao público como senhas de atendimento. Examinando-se esses cartões, observou-se que

• 20 deles tinham numeração múltipla de 3;

• 15 deles tinham numeração múltipla de 4;

• 10 deles tinham numeração múltipla de 12.

Considerando-se que a caixa contém o menor número possível de cartões com essas características, pode-se afirmar que, retirando-se, aleatoriamente, um desses cartões, a probabilidade de que ele não tenha numeração múltipla de 12 é igual a