Em determinado tribunal, a data em que cada processo é protocolado marca a data inicial deste, a partir da qual é contada a quantidade de meses que se passam até que o juiz apresente a decisão final sobre ele. Essa quantidade de meses é uma variável aleatória X cuja função densidade de probabilidade é dada por 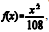, para 0 < x ≤ 6, e 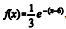, para x > 6, em que e é o número de Euler, base dos logaritmos neperianos.

A partir dessas informações, julgue o item a seguir.

Sabendo-se que 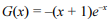é primitiva de 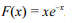, conclui-se que, no tribunal em questão, é superior a seis meses o tempo médio esperado até a decisão final para os processos protocolados

Em determinado tribunal, a data em que cada processo é protocolado marca a data inicial deste, a partir da qual é contada a quantidade de meses que se passam até que o juiz apresente a decisão final sobre ele. Essa quantidade de meses é uma variável aleatória X cuja função densidade de probabilidade é dada por 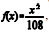, para 0 < x ≤ 6, e 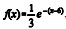, para x > 6, em que e é o número de Euler, base dos logaritmos neperianos.

A partir dessas informações, julgue o item a seguir.

A probabilidade de que o juiz responsável por certo processo leve entre três e sete meses para apresentar sua decisão final é igual a .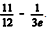

Em determinado tribunal, a data em que cada processo é protocolado marca a data inicial deste, a partir da qual é contada a quantidade de meses que se passam até que o juiz apresente a decisão final sobre ele. Essa quantidade de meses é uma variável aleatória X cuja função densidade de probabilidade é dada por , para 0 < x ≤ 6, e , para x > 6, em que e é o número de Euler, base dos logaritmos neperianos.

A partir dessas informações, julgue o item a seguir.

A probabilidade de que o juiz responsável por certo processo leve mais de seis meses para apresentar sua decisão final é inferior a 30%.

Em determinado tribunal, a data em que cada processo é protocolado marca a data inicial deste, a partir da qual é contada a quantidade de meses que se passam até que o juiz apresente a decisão final sobre ele. Essa quantidade de meses é uma variável aleatória X cuja função densidade de probabilidade é dada por, para 0 < x ≤ 6, e , para x > 6, em que e é o número de Euler, base dos logaritmos neperianos.

A partir dessas informações, julgue o item a seguir.

Conforme a situação apresentada, P(X = 6) > P(X = 5).

Em determinado tribunal, a data em que cada processo é protocolado marca a data inicial deste, a partir da qual é contada a quantidade de meses que se passam até que o juiz apresente a decisão final sobre ele. Essa quantidade de meses é uma variável aleatória X cuja função densidade de probabilidade é dada por, para 0 < x ≤ 6, e , para x > 6, em que e é o número de Euler, base dos logaritmos neperianos.

A partir dessas informações, julgue o item a seguir.

A probabilidade de que o juiz leve três meses para apresentar sua decisão final a respeito de determinado processo é inferior a 10%.