A “Lei de resfriamento de Newton” consiste de um modelo simples para a dinâmica da temperatura T de um corpo inicialmente a uma temperatura T₀ , que troca calor com o ambiente, a uma temperatura TR < T₀, em uma taxa proporcional apenas à diferença entre a temperatura do corpo e do meio exterior. A taxa de condução do calor entre o corpo e o meio que depende de características físicas como a superfície de contato entre o corpo e o meio é contabilizada em termos efetivos pela constante positiva k. A equação do modelo está representada na imagem abaixo. No gráfico temos o resultado do experimento conduzido para uma pequena quantidade de glicerina (10 cm³ ) em um tubo de ensaio a uma temperatura inicial T₀ =100ºC sendo a temperatura do ambiente TR = 21ºC. O perfil observado é aproximadamente exponencial. Considerando 1/e = 0,37. O valor da constante k para esse experimento é de aproximadamente:

A variação do volume de bolhas de ar em um meio líquido como o sangue depende da pressão do meio externo sobre as paredes da bolha e está associada a problemas graves de saúde como a embolia pulmonar gasosa, e consiste de um problema muito estudado na literatura médica, biológica e biofísica. Considere que pequenas bolhas de gás ideal são formadas no fundo de um recipiente com uma coluna de água de 20cm. Ao se desprenderem do fundo irão pela ação do empuxo serem trazidas à superfície que está à pressão de 1atm = 105 Pa. Considere a densidade da água de 1000 kg/m³ e g = 10m/s² . A temperatura do fluido ao longo do recipiente é constante. O aumento percentual no volume da bolha será de:

Considere uma barragem plana como a do esquema da Figura. 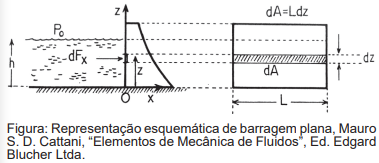O elemento diferencial da força exercida pelo fuido a uma altura z em relação ao fundo segue a expressão dF = p(z)dA, com dA = Ldz (elemento de área da barragem de largura L). A pressão p(z) é dada pela lei (ou teorema) de Stevin. A partir da integração da força ao longo da coordenada z de z=0 até a altura da coluna d’água, z=h temos a força total exercida pela coluna de água de altura h sobre a barragem. Considere uma barragem de comprimento L=20m, h=20m, e os valores de densidade da água de d=1000kg/ m³ e g=10m/s² . A expressão matemática da força total sobre a barragem devida a coluna d’água e seu valor físico para essa particular barragem são dados por:

Para determinar a velocidade do som em um experimento didático simples foram analisadas as ondas de som estacionárias (harmônicos) produzidas em um tubo cilíndrico aberto de 20cm geradas a partir de um tapa dado em uma de suas extremidades. Durante a produção do som um dos lados do tubo fica fechado pela mão. O espectro sonoro foi captado através de um microfone introduzido dentro do tubo e ligado a um software de análise das intensidades de cada frequência, sendo obtido o espectro sonoro da figura. Considere a velocidade de propagação da onda de som utilizando as medidas do primeiro e o terceiro harmônico apenas, o valor médio delas é de aproximadamente:

No diagrama abaixo temos o desenho em escala de um automóvel. As linhas cinzas indicam a posição das molas dianteiras e traseiras bem como do centro de massa do automóvel (posicionado na intersecção entre as duas faixas cinzas correspondentes). Em virtude do motor ser um dos componentes de maior massa em carros de tração dianteira o centro de massa em geral fica mais próximo da frente (onde ele é disposto) do que da traseira. Admita que as molas tanto traseiras quanto dianteiras tenham mesmo comprimento e que o carro é regulado para estar no nível (prumo) com a mesma compressão sobre todas elas. Sobre as constantes elástica das molas dianteiras, k_D, e traseiras, k_T, assinale a alternativa correta.