Questões do concurso:
CBM-RJ - 2021 - CBM-RJ - 2021 - Aspirante
limpar filtros
50 Questões de concurso encontradas
Página 5 de 10
Questões por página:
Questões por página:
Algumas medidas preventivas podem ser adotadas contra infecções respiratórias provocadas por vírus em seres humanos.
Uma dessas medidas é:
Uma dessas medidas é:
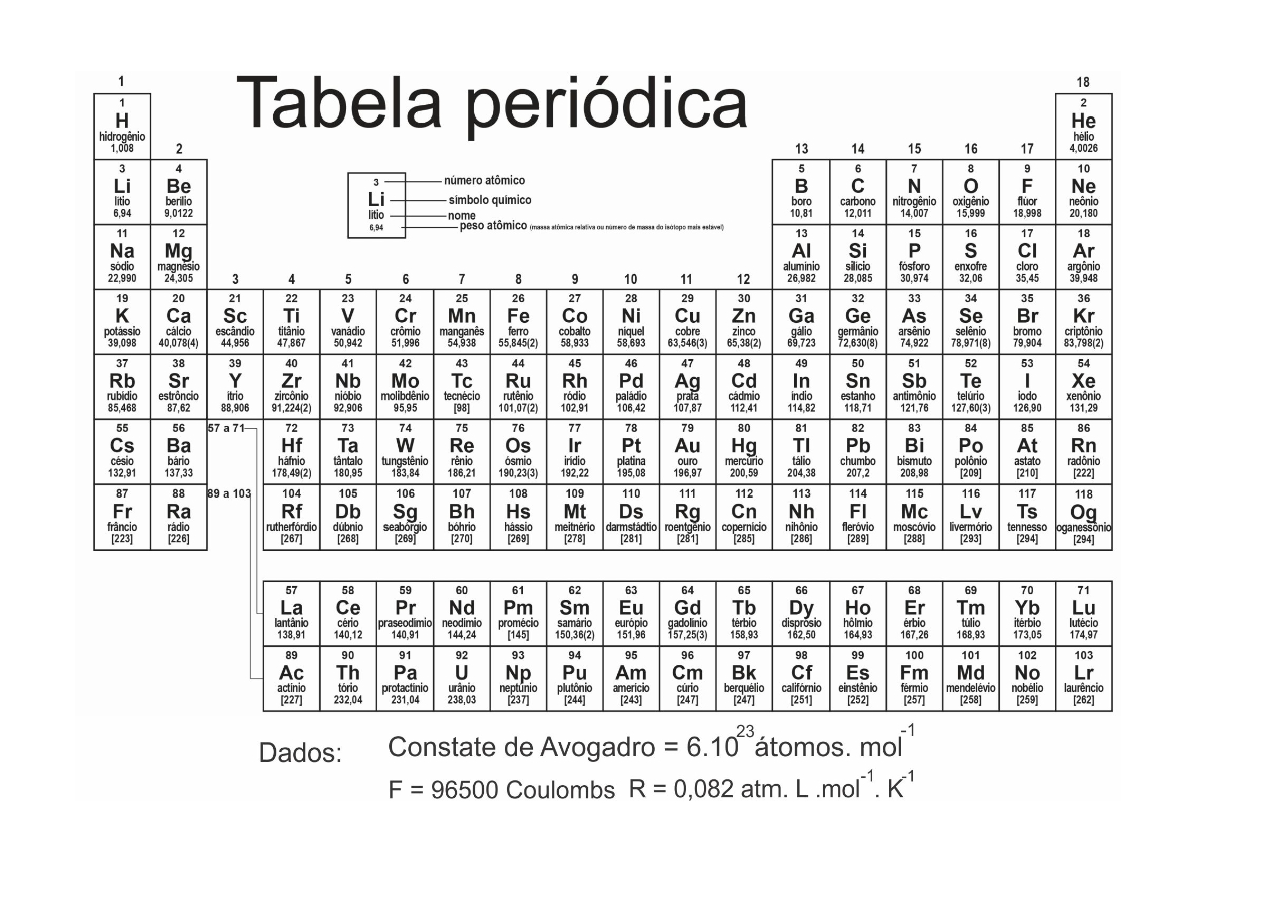
A reação química entre o dióxido de nitrogênio e a água acarreta a formação de uma mistura de dois ácidos, comumente empregada na produção de fertilizantes. A equação química a seguir representa essa reação.
2 NO2 + H2O → HNO2 + HNO3
Analisando apenas os compostos participantes da reação, o maior número de oxidação do nitrogênio corresponde a:
Concurso:
CBM-RJ
Disciplina:
Matemática
Dois dados com a forma de tetraedros regulares apresentam em suas faces os números 1,2,3 e 4, sendo um por face. Lançando-se os dois dados ao acaso, cada face tem a mesma probabilidade de ficar virada para baixo.

Após um lançamento, a probabilidade de a soma de todos os números visíveis, nos dois dados, ser maior do que quinze é igual a:

Após um lançamento, a probabilidade de a soma de todos os números visíveis, nos dois dados, ser maior do que quinze é igual a:
Concurso:
CBM-RJ
Disciplina:
Matemática
Durante o voo, um pássaro inclina as asas de θ graus em relação ao plano horizontal, como indica a figura 1. Com essa inclinação, ele percorre um arco de circunferência em um plano paralelo ao horizontal.
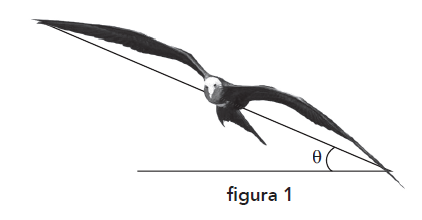
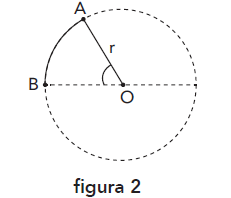
Considere que o pássaro inclinou suas asas de θ = 30º, percorrendo um arco de circunferência AB, representado na figura 2, de modo que o ângulo central AÔB = 60º e que tgθ = 6/ r .
Com as aproximações π ≅ 3 e √3 ≅ 1,7, o comprimento do arco AB, em metros, está mais próximo de:

Considere que o pássaro inclinou suas asas de θ = 30º, percorrendo um arco de circunferência AB, representado na figura 2, de modo que o ângulo central AÔB = 60º e que tgθ = 6/ r .

Com as aproximações π ≅ 3 e √3 ≅ 1,7, o comprimento do arco AB, em metros, está mais próximo de:
Concurso:
CBM-RJ
Disciplina:
Matemática
Seis fichas numeradas de 1 a 6 serão dispostas em um tabuleiro com nove casas, conforme ilustrado a seguir. Cada ficha deve ocupar uma única casa, e cada casa não pode ser ocupada por mais do que uma ficha. Em cada disposição, as fichas com número ímpar devem ocupar uma única fila horizontal.
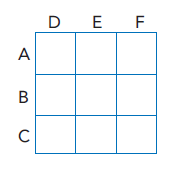
O número total de modos possíveis de dispor as seis fichas é igual a:

O número total de modos possíveis de dispor as seis fichas é igual a: