Questões de Concurso
Filtrar
1.392 Questões de concurso encontradas
Página 81 de 279
Questões por página:
Seja 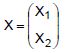 um vetor de variáveis aleatórias e seja
um vetor de variáveis aleatórias e seja 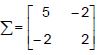 sua matriz de covariâncias. Seja Y a segunda componente principal da matriz Σ. A proporção da variância total de X que é explicada por Y é
sua matriz de covariâncias. Seja Y a segunda componente principal da matriz Σ. A proporção da variância total de X que é explicada por Y é
Considere o modelo de séries temporais dado por Zt = 0,6 Zt-1 + at, onde at é o ruído branco de média zero e variância 4.
Nessas condições, a variância de Zt é
Desejando-se estimar a proporção p de pessoas favoráveis a certo projeto governamental numa população, utilizou-se a proporção amostral p , com base numa amostra aleatória simples, com reposição de 200 observações. Se temos a informação que 0 = p = 0,4, e se var (![]() ) representa a variância de
) representa a variância de ![]() , então
, então
Três máquinas: A, B e C de uma determinada indústria produzem a totalidade das peças de certo tipo que são utilizadas na fabricação de um motor de um automóvel. Sabe-se que a A e B produzem cada uma 30% das peças e C produz 40%. Sabe-se que 5%, 10% e 2%, respectivamente, das produções de A, B e C são defeituosas. Uma peça é selecionada, aleatoriamente, da produção conjunta das três máquinas. A probabilidade de ela ter sido fabricada por A, sabendo-se que é defeituosa, é