Questões de Concurso
Filtrar
250 Questões de concurso encontradas
Página 28 de 50
Questões por página:
Questões por página:
Concurso:
CBM-SC
Disciplina:
Matemática
Para ter acesso às suas notas, os alunos de uma determinada escola recebem um login e uma senha. O login é o número de matrícula do aluno e a senha é seu primeiro nome. O número da matrícula é formado por duas vogais distintas e número de quatro algarismos distintos e divisíveis por cinco. De quantas maneiras possíveis pode ser gerado um número de matrícula nessa escola?
Concurso:
CBM-SC
Disciplina:
Matemática
As irmãs Isadora e Isabela farão uma viagem em janeiro de 2016. Para isso resolveram guardar uma quantia de dinheiro todos os meses no período de janeiro a dezembro de 2015. A primeira quantia que cada uma guardou foi de R$ 200,00 e a cada mês será acrescido ao valor a ser guardado o correspondente a 40% da primeira quantia. Qual será o valor guardado pelas duas irmãs em dezembro de 2015?
Concurso:
CBM-SC
Disciplina:
Matemática
Em uma atividade na quadra da escola, a professora de matemática distribuiu três alunos onde cada um representava o vértice de um triângulo da quadra. Cada aluno possuía uma coordenada; analise‐as. 
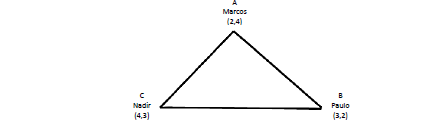
A professora pediu aos outros alunos que calculassem a área do triângulo formado pelos três alunos. Qual o valor daárea encontrada pelo restante da turma?
Concurso:
CBM-SC
Disciplina:
Matemática
Os amigos Artur, Bernardo e Carlos treinam natação diariamente. O treino de hoje foi dividido em três etapas. O sistema a seguir indica o número de voltas que cada amigo nadou em cada etapa.
De acordo com os valores encontrados, é correto afirmar que
Concurso:
CBM-SC
Disciplina:
Matemática
Todas as manhãs João caminha no parque ao lado de seu prédio e o observa. Ele analisou que ao observar seu prédio de um ângulo 30° este estava a 50 metros, na horizontal, de distância. Quando o ângulo de observação passa a ser de 60° a distância entre João e o prédio é de x metros na horizontal. Sabendo que a altura dos olhos de João ao solo é 1,50, m a altura do prédio e a distância x valem, respectivamente: (Considere: √3 = 1,7.)