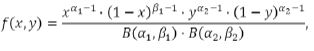Questões de Concurso
Filtrar
1.843 Questões de concurso encontradas
Página 177 de 369
Questões por página:
Questões por página:
Concurso:
TJ-ES
Disciplina:
Estatística
mostrar texto associado
A função ![]() em que
em que ![]() são as densidades de X e Y, e C'(u, v) é a derivada da função
são as densidades de X e Y, e C'(u, v) é a derivada da função
C(u, v), é a densidade conjunta.
Concurso:
TJ-ES
Disciplina:
Estatística
mostrar texto associado
Se ![]() e
e ![]() se (x, y) segue uma distribuição F(x, y) = C(FX(x), FY(y)), então X e Y são dependentes.
se (x, y) segue uma distribuição F(x, y) = C(FX(x), FY(y)), então X e Y são dependentes.
Concurso:
TJ-ES
Disciplina:
Estatística
Julgue o item abaixo sabendo que sen 0 = cos π/2 = 0, que ∫ sen x dx = − cos x e que ∫ cos x dx = sen x .
Para que a função ![]() definida para 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, seja uma densidade conjunta de probabilidade, é necessário que k seja igual a 1/8 π2.
definida para 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, seja uma densidade conjunta de probabilidade, é necessário que k seja igual a 1/8 π2.
Concurso:
TJ-ES
Disciplina:
Estatística
mostrar texto associado
A covariância entre X e Y é nula.
Concurso:
TJ-ES
Disciplina:
Estatística
mostrar texto associado
Se a distribuição estiver definida dentro do quadrado [0,1] × [0,1], então a probabilidade de uma realização (x, y) estar dentro do círculo de centro (½, ½) e raio ½ será igual a π/4.