Questões de Concurso
Filtrar
2.465 Questões de concurso encontradas
Página 428 de 493
Questões por página:
Uma empresa aérea, analisando os seus dados históricos, sabe que aproximadamente 5% dos passageiros que fizeram reserva em um determinado voo não aparecerão (perderão o voo). Consequentemente, a política da empresa é vender 62 assentos para um voo que comporta apenas 60 passageiros. A empresa deseja, assim, saber qual é a probabilidade, P, de haver um assento disponível para cada passageiro que aparecerá na hora com a intenção de embarcar.
Um modo de se obter a média de uma variável aleatória é usando a sua distribuição cumulativa. Sabendo-se assim que a variável aleatória X é uniformemente distribuída no intervalo (0,1), calcule o valor esperado da variável aleatória X3, isto é: E[X3 ].
Uma determinada empresa aérea tem sofrido atrasos nos seus voos devido à falta de programação a respeito das possíveis falhas que podem ocorrer nos seus aviões. Falhas frequentes incluem desde trincas nos trens de pousos até mesmo falhas imprevistas nas suas turbinas. Apesar de possuir um certo estoque de turbinas, não se sabe na empresa qual ou quais falhas ocorrerão primeiro. Decidiu-se então fazer um estudo e observou-se que os intervalos das falhas, tanto nas turbinas quanto nas trincas nas asas (que requerem manutenção, paralisando o uso dos aviões) ocorrem de acordo com taxas exponenciais, com intervalos de tempo de 15 dias para uma falha de turbina e de um mês para as trincas das asas. Em virtude do estoque das turbinas, uma falha em uma única turbina não é tão preocupante, mas falha em duas turbinas, mesmo que sejam em aviões diferentes, já podem atrasar os trabalhos das equipes de manutenção. Descreva os possíveis eventos do seguinte modo: Eji, ou seja, j eventos ocorrem no processo Ni (t).
Desse modo, a empresa aérea quer saber o valor da seguinte probabilidade: P{E21 < E1 2 }. Mais especificamente, indique a probabilidade de duas turbinas falharem, antes que uma trinca nas asas, que requer manutenção, ocorra (j=2 e evento i=1 – falha das turbinas, e j=1 e evento 2 – trinca das asas).
Com o objetivo de utilizar as suas aeronaves de um modo mais eficiente, uma determinada empresa aérea deseja aplicar um mesmo modelo de otimização para as suas diferentes rotas. Entretanto, esse mesmo modelo só funcionará, principalmente, se as variâncias dessas diferentes rotas puderem ser consideradas as mesmas. Para simplificar, a empresa aérea decidiu comparar apenas duas das suas rotas, que possuem os seguintes dados anuais:
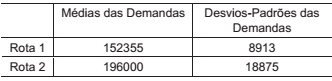
De acordo com os dados acima, foi realizado o seguinte teste de Hipóteses para um teste de significância α = 5%:
H0 : σ12 =σ22
H1 : σ12 ≠ σ22
Além disso, os tamanhos das amostras usadas para se obter as médias e desvios-padrões acima foram de 25 e 30 para as amostras 1 e 2, respectivamente. Aplicando o teste de Hipótese, pode-se então concluir que:
yt = 1,2 yt-1 – 0,19 yt-2 + εt
Sabendo que os valores reais das demandas nos tempos t–1 e t–2 foram de 11300 e 12250 passageiros, respectivamente, calcule os valores dos resíduos para os tempos t e t+1, assumindo uma previsão estática.