60 Questões de concurso encontradas
Página 1 de 12
Questões por página:
Seja Z = (X,Y) uma variável aleatória com distribuição normal bivariada com vetor de médias μ = 
e matriz de covariâncias 
. Para uma amostra aleatória simples (Xi, Yi), i = 1, 2, 3, 4 da distribuição de Z, sejam 
.
O valor de K para que a diferença, em valor absoluto, entre 
seja superior a K, com probabilidade de 4% , é
Seja X o consumo mensal de água por residência de um bairro de determinada cidade. Sabe-se que X tem distribuição Normal com μ = 10 m3 e σ = 2 m3. Seja 
a média amostral de uma amostra de n residências, selecionadas aleatoriamente e com reposição. Sabendo que P (|- 10 | < 0,5 )= 0,788 , o valor de n é
O tempo total de montagem de uma peça mecânica tem distribuição normal e é dado pela soma dos tempos das 3 etapas necessárias para a sua conclusão. Sejam Xi , i = 1, 2, 3, as variáveis aleatórias que representam os tempos de montagem das etapas 1, 2 e 3, respectivamente. Sabe-se que essas variáveis são independentes e que têm distribuição normal com parâmetros dados na tabela abaixo: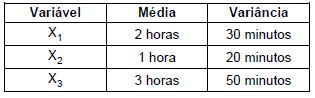 
A probabilidade de a peça levar entre 374 e 384 minutos para ser montada é igual a
