150 Questões de concurso encontradas
Página 4 de 30
Questões por página:
O tempo médio de contribuição previdenciária e a média da idade do trabalhador são, respectivamente, iguais a λ2φ e φ.
Acerca dessa situação hipotética, julgue o item que se segue.
A distribuição da idade do trabalhador é 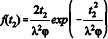 ,
,
Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a µt = (– 5, 0, 5) e matriz de covariância 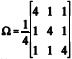 . Com base nessas informações, julgue o item subseqüente.
. Com base nessas informações, julgue o item subseqüente.
Considere a matriz aleatória Y = [y1, y2], em que y1 e y2 são vetores aleatórios independentes e com a mesma distribuição de x - µ. Nessa situação, YYt segue uma distribuição de Wishart com 2 graus de liberdade.
Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a µt = (– 5, 0, 5) e matriz de covariância 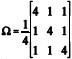 . Com base nessas informações, julgue o item subseqüente.
. Com base nessas informações, julgue o item subseqüente.
Considere-se  e E = [e1, e2, e3], em que λ1, λ2 e λ3 são os autovalores de Ω e e1, e2 e e3 são os respectivos autovetores padronizados. Nessa situação, o vetor aleatório (E ∧Et ) (x - µ) segue uma distribuição normal cuja matriz de covariância é igual à matriz identidade.
e E = [e1, e2, e3], em que λ1, λ2 e λ3 são os autovalores de Ω e e1, e2 e e3 são os respectivos autovetores padronizados. Nessa situação, o vetor aleatório (E ∧Et ) (x - µ) segue uma distribuição normal cuja matriz de covariância é igual à matriz identidade.
Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a µt = (– 5, 0, 5) e matriz de covariância 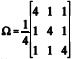 . Com base nessas informações, julgue o item subseqüente.
. Com base nessas informações, julgue o item subseqüente.
Considerando os vetores transpostos v1t = (– 5, 0, 0) e v2t = (0, 0, 0), o quadrado da distância de Mahalanobis entre ambos é superior a 30 e inferior a 60.
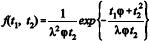 , em que t1 > 0, t2 > 0, exp( ·) representa a função exponencial, λ > 0, e φ > 0 são os parâmetros da distribuição.
, em que t1 > 0, t2 > 0, exp( ·) representa a função exponencial, λ > 0, e φ > 0 são os parâmetros da distribuição.