Sabe-se que uma urna contém uma proporção de p bolas pretas e de (1 - p) bolas brancas. O valor de p é desconhecido, mas sabe-se que é 3/5 ou é 1/2. A fim de se chegar a uma conclusão, seleciona-se ao acaso e com reposição 10 bolas da urna e observa-se o número de bolas pretas. Um teste de hipóteses é proposto, esse considera testar a hipótese nula H₀: p = 1/2 contra a hipótese alternativa H_a: p = 3/5. Se o teste rejeitar H₀ quando pelo menos 8 bolas pretas forem encontradas, o nível de significância do teste é igual a

Um relatório, redigido por um auditor de um órgão público, tem 2 capítulos com 40 páginas cada. Esse relatório apresenta uma média de 1 erro ortográfico a cada 10 páginas. Considere que:

I. a variável X que representa o número de erros por página tem distribuição de Poisson com média 0,1;
II. existe independência entre os eventos número de erros ortográficos do capítulo 1 e número de erros ortográficos do capítulo 2.

Nessas condições, a probabilidade de que pelo menos um dos capítulos possua no máximo um erro ortográfico é igual a

Dados:
e^-0,1 = 0,905
e^-2 = 0,135
e^-4 = 0,018

Se Z tem distribuição normal padrão, então:
P(Z < 0,4) = 0,655; P(Z < 1,2) = 0,885; P(Z < 1,6) = 0,945; P(Z < 1,8) = 0,964; P(Z < 2) = 0,977.

O efeito do medicamento A é o de baixar a pressão arterial de indivíduos hipertensos. O tempo, em minutos, decorrido entre a tomada do remédio e a diminuição da pressão é uma variável aleatória X com distribuição normal, tendo média µ e desvio padrão σ.

Se o valor de µ é de 56 min e o valor de s é de 10 min, a probabilidade de X estar compreendido entre 52 min e 74 min é igual a

Se Z tem distribuição normal padrão, então:

P(Z < 0,4) = 0,655; P(Z < 1,2) = 0,885; P(Z < 1,6) = 0,945; P(Z < 1,8) = 0,964; P(Z < 2) = 0,977.

O efeito do medicamento A é o de baixar a pressão arterial de indivíduos hipertensos. O tempo, em minutos, decorrido entre a tomada do remédio e a diminuição da pressão é uma variável aleatória X com distribuição normal, tendo média µ e desvio padrão σ.

Uma amostra aleatória de n indivíduos hipertensos foi selecionada com o objetivo de se estimar µ. Supondo que o valor de s é 10 min, o valor de n para que o estimador não se afaste de µ por mais do que 2 min, com probabilidade de 89%, é igual a

Se Z tem distribuição normal padrão, então:

P(Z < 0,4) = 0,655; P(Z < 1,2) = 0,885; P(Z < 1,6) = 0,945; P(Z < 1,8) = 0,964; P(Z < 2) = 0,977.

Uma auditoria feita em uma grande empresa considerou uma amostra aleatória de 64 contas a receber. Se a população de onde essa amostra provém é infinita e tem distribuição normal com desvio padrão igual a R$ 200,00 e média igual a R$ 950,00, a probabilidade da variável aleatória média amostral, usualmente denotada por 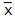, estar situada entre R$ 980,00 e R$ 1.000,00 é dada por