Questões da prova:
FCC - 2018 - TRT - 14ª Região (RO e AC) - Analista Judiciário - Estatística
limpar filtros
60 Questões de concurso encontradas
Página 6 de 12
Questões por página:
Questões por página:
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Um intervalo de confiança com um nível de (1 − α) foi construído para a média μ1 de uma população P1, normalmente distribuída, de tamanho infinito e variância populacional igual a 144. Por meio de uma amostra aleatória de tamanho 36 obteve-se esse intervalo igual a [25,3; 34,7]. Seja uma outra população P2, também normalmente distribuída, de tamanho infinito e independente da primeira. Sabe-se que a variância de P2 é conhecida e que por meio de uma amostra aleatória de tamanho 64 de P2 obteve-se um intervalo de confiança com um nível de (1 − α) para a média μ2 de P2 igual a [91,54; 108,46]. O desvio padrão de P2 é igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Uma variável aleatória X tem a seguinte função de densidade:

Obs.: Se ln(a) é o logaritmo neperiano de a então: ln(0,50) = −0,69, ln(0,70) = −0,36, ln(0,80) = −0,22 e ln(0,72) = −0,33.
A estimativa encontrada para K, com base na amostra, foi de
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Questão Anulada
Com base em uma amostra aleatória de tamanho 12 obtiveram-se, pelo método dos momentos, as estimativas pontuais dos parâmetros a e b de uma variável aleatória X uniformemente distribuída no intervalo (a, b), sendo 0 < a < b. A média amostral 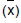 apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
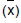 apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
Os estimadores independentes e não viesados E1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
Concurso:
TRT - 14ª Região (RO e AC)
Disciplina:
Estatística
A média de uma variável aleatória X, cuja distribuição é desconhecida, é igual a m, com m > 0. Pelo Teorema de Tchebichev, a probabilidade de X não pertencer ao intervalo (m − θ, m + θ), com m > θ, é no máximo igual a 16%. O desvio padrão de X é então igual a θ multiplicado por