Em uma determinada indústria, foi efetuada uma pesquisa a respeito da possível relação entre o número de horas trabalhadas (X), com X ≥ 2, e as quantidades produzidas de um produto (Y). Com base em 10 pares de observações (X_i, Y_i) e considerando o gráfico de dispersão correspondente, optou-se por utilizar o modelo linear Y_i = α + βX_i + ε_i, com i representando a i-ésima observação, ou seja, i = 1,2,3, ...10. Os parâmetros α e β são desconhecidos e as suas estimativas (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados. Observação: ε_i é o erro aleatório com as respectivas hipóteses do modelo de regressão linear simples. Considere o gráfico, abaixo, construído utilizando os valores encontrados para as estimativas de α e β.

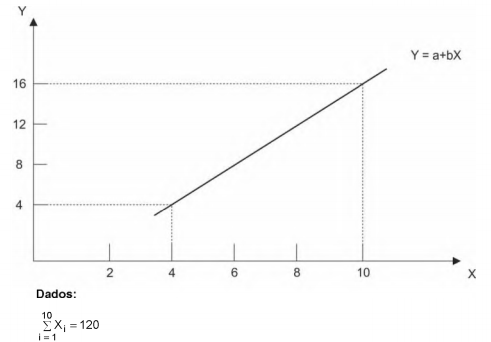
A previsão da quantidade produzida será igual ao dobro da média verificada das 10 observações Y_i quando o número de horas trabalhadas for igual a

Um curso de treinamento é ministrado para os profissionais de determinado ramo de atividade. A população das notas de avaliação no curso, que é considerada de tamanho infinito e normalmente distribuída, apresenta uma média μ igual a 7 e variância σ² igual a 4. Acredita-se que mediante um processo de aperfeiçoamento no curso, essa média tenha sido aumentada. Para analisar a eficácia desse processo foi extraída uma amostra aleatória de tamanho 64 da população após o processo de aperfeiçoamento e foram formuladas as hipóteses H₀: μ = 7 (hipótese nula) e H₁: μ > 7 (hipótese alternativa). O valor encontrado para a média amostral (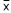 ) foi o maior valor tal que, ao nível de significância de 5%, H₀ não foi rejeitada. Tem-se que 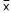é igual a

Uma variável aleatória X representa o número de contribuintes que chega a cada hora para ser atendido em um órgão público. Supõe-se que X tem distribuição de Poisson, com parâmetro λ, ou seja, , sendo e a base do logaritmo (ln) tal que ln(e) = 1. Se P(x = 2) = P(x = 3), então a probabilidade de que menos de 3 contribuintes cheguem em 1 hora é

Dados:

e^-1 = 0,37,

e^-2 = 0,14 e

e^-3 = 0,05

Considere a distribuição dos salários, em R$ 1.000,00, dos funcionários lotados em uma repartição pública, representada abaixo pela tabela de frequências relativas acumuladas, sendo k a frequência relativa acumulada do 4° intervalo de classe.

Sabe-se que a média aritmética (Me) foi calculada considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio desse intervalo, que a mediana (Md) foi calculada pelo método da interpolação linear e que a moda (Mo) foi obtida pela relação de Pearson, ou seja, Mo = 3Md - 2Me. Dado que Me = R$ 7.200,00, então Mo é igual a