Para estimar a proporção p de eleitores que, em um dado momento, pretendiam votar em certo candidato em uma eleição futura, uma amostra de 625 eleitores foi observada e constatou-se que, na amostra,312 eleitores disseram que pretendiam votar no candidato.

Um intervalo aproximado de 99% de confiança para p é dado por

Uma amostra aleatória simples de tamanho 400 foi obtida de uma variável aleatória populacional, com média µ desconhecida e apresentou os seguintes resultados:

Média amostral: 125

Variância amostral: 100

Um intervalo aproximado com 95% de confiança para µ será dado por

Avalie se 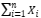é uma estatística suficiente para o parâmetro indicado nos casos a seguir.

I. Uma distribuição Bernoulli para a qual o parâmetro p (0 < p < 1) é desconhecido.

II. Uma distribuição geométrica para a qual o parâmetro p (0 < p < 1) é desconhecido.

III. Uma distribuição normal com média conhecida e variância σ² desconhecida.

Está correto o que se afirma em

Avalie se as seguintes famílias de distribuições são uma família exponencial:

I. A família de distribuições Poisson com média desconhecida.

II. A família de distribuições normais com média conhecida e variância desconhecida.

III. A família de distribuições Beta com parâmetro α conhecido e parâmetro β desconhecido.

IV. A família de distribuições Uniforme no intervalo (0, θ), θ parâmetro desconhecido.

São de fato famílias exponenciais

Avalie se as afirmativas a seguir, relacionadas à estimação por máxima verossimilhança de um parâmetro θ, são falsas (F) ou verdadeiras (V).

( ) A função de verossimilhança de um conjunto de variáveis aleatórias é definida como a função de densidade (ou de probabilidade) conjunta dessas variáveis olhada como função de θ.

( ) Se X₁, X₂, ..., X_n é uma amostra aleatória simples de uma densidade uniforme no intervalo (0, θ), o estimador de máxima verossimilhança de θ é máx{Xi}, ou seja, é a n-ésima estatística de ordem.

( ) Se X₁, X₂, ..., X_n é uma amostra aleatória simples de uma densidade N(µ, σ² ), σ conhecida, o estimador de máxima verossimilhança de µ é a média amostral.

Na ordem apresentada, as afirmativas são, respectivamente,