Questões da prova:
FGV - 2015 - TJ-RO - Analista Judiciário - Estatística
limpar filtros
70 Questões de concurso encontradas
Página 4 de 14
Questões por página:
Questões por página:
Concurso:
TJ-RO
Disciplina:
Estatística
Sejam X, Y e Z variáveis aleatórias tais que Var (X) = Var (Y) = Var (Z) = 6, Cov (X, Y) = -3 e Z não correlacionada com as outras duas. Logo, a variância de W = 3X – 2Y + Z é igual a:
Concurso:
TJ-RO
Disciplina:
Estatística
Seja X uma variável aleatória contínua com função distribuição acumulada Fx (x) Outra variável, Y, é definida por Y = Fx (x) Então a distribuição acumulada de Y é dada por:
Concurso:
TJ-RO
Disciplina:
Estatística
Seja X = número de anos de condenação e Y = nível de renda do condenado (mil reais). São fornecidas ainda as seguintes informações:
Var(X) = 25; Var (Y) = 16 e Var (X+Y) = 21
Assim sendo, a correlação (Pearson) entre X e Y é igual a:
Concurso:
TJ-RO
Disciplina:
Estatística
Considere a distribuição conjunta abaixo:
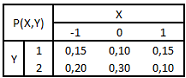
Então, P(X > -1/Y < 2) e E(X/Y =2) são respectivamente iguais a:
Concurso:
TJ-RO
Disciplina:
Estatística
Suponha que X e Y são variáveis aleatórias independentes, definidas no mesmo intervalo, com funções de densidade fx(x) e fy(y), respectivamente. Então a função de densidade conjunta, naquele intervalo, é dada por: