2. Questões de Concurso
  3. Questões da Prova
CESGRANRIO - 2011 - TRANSPETRO - Químico de Petróleo Júnior
limpar filtros
Questões por página:

A figura abaixo mostra o gráfico de uma função derivável f:(- 4,4)→ IR.



O reconhecimento dos intervalos de crescimento e decrescimento da função f(x) fornece informações sobre os sinais de sua derivada, f' :(- 4,4)→ IR.
No que se refere a tais informações, um gráfico admissível para a função f' seria



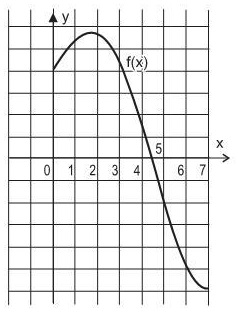
A figura acima mostra, no plano cartesiano, o gráfico de uma função contínua f:[0,7]→ IR, disposto sob uma malha quadriculada. Observando o gráfico, considere as afirmações a seguir.
 
A integral ∫ 70 f(x) dx é positiva.
 
PORQUE
 
O valor da integral definida de uma função contínua é igual a uma área.
 
Analisando-se as afirmações acima, conclui-se que
Duas funções deriváveis, f, g:IR→ IR, são tais que f'(x)= g'(x) / 2, ∀x∈ IR.
 
Se f(x) = 3, f(5) = 9 e g(1) = -4, quanto vale g(5)?
O ciclo percorrido por um fluido em uma máquina de Carnot é representado por
Uma isoterma de adsorção representa a quantidade de um gás adsorvido por um sólido em função da pressão de equilíbrio, a temperatura constante. Sendo θ a fração da superfície do sólido ocupada pelo gás, P a pressão de equilíbrio e K a constante de equilíbrio de adsorção, respectivamente, e considerando as hipóteses formuladas por Langmuir para descrever o fenômeno de adsorção: as entidades adsorvidas estão ligadas à superfície do sólido em locais fixos, cada centro ativo da superfície só pode acomodar uma entidade adsorvida e a adsorção é energeticamente idêntica em todos os centros ativos e independente da presença ou ausência de espécies adsorvidas na sua vizinhança, a equação que representa a isoterma de Langmuir é
© 2016-2024 Fonte Concursos - Questões de Concurso e Plano de Estudo