70 Questões de concurso encontradas
Página 5 de 14
Questões por página:
Seja X uma variável aleatória contínua e Y= G(X) uma função de X tal que, no domínio da fx(x), densidade da X, as derivadas de 1ª e de 2ª ordem da G(X) são estritamente negativas. Considerando,
fy(y)= função densidade de probabilidade de Y;
fx-1(x) = função inversa da densidade de X;
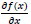 = derivada de f(x) com respeito à x;
= derivada de f(x) com respeito à x;
E(X) = esperança matemática de X;
h[f(X)] = função composta de f com h.
Então é correto afirmar que:
A capacidade de um time de futebol de marcar gols em uma única partida é uma variável aleatória. A tabela a seguir apresenta a probabilidade de certo time marcar um número mínimo (Y) de gols em uma partida:

Isso significa que o número médio de gols marcados por esse time em uma única partida de futebol é igual a:
Seja X uma variável aleatória mista com função densidade de probabilidade dada por:
fx(x) = 1/x2 para 1< x ≤ 4, P(X = 1 ) = 0,25, sendo igual azero caso contrário.
Então os valores de P ( X ≤ 2 ) e E (X2) , esperança matemática de X ao quadrado, são respectivamente iguais a: