Questões da prova:
IBFC - 2017 - SEDUC-MT - Professor - Matemática
limpar filtros
70 Questões de concurso encontradas
Página 2 de 14
Questões por página:
Questões por página:
A Etnomatemática pode ser considerada uma abordagem histórico-cultural da disciplina, na qual a matemática deve ser compreendida não apenas como uma constituição social, mas também como uma construção histórica e política. Analise as seguintes afirmações acerca da Etnomatemática: I. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos. II. a Etnomatemática não se trata de um método de ensino nem de uma nova ciência, mas de uma proposta educacional que estimula o desenvolvimento da criatividade, conduzindo a novas formas de relações interculturais. III. A Etnomatemática trata-se de uma vertente que busca identificar manifestações matemáticas nas culturas periféricas e tem como referências categorias própria de cada cultura.
Assinale a alternativa que indica quais destas afirmações estão corretas:
Assinale a alternativa que indica quais destas afirmações estão corretas:
No contexto da Aritmética, a divisão de um valor não nulo por zero é considerada indefinida. Abaixo seguem alguns argumentos, utilizando os números naturais, apresentados por um professor a seus alunos, para demonstrar que essa divisão seria indefinida:
I. Ao se dividir objetos entre pessoas, como se atribuir algo a nenhuma pessoa? Por exemplo, ao se dividir seis doces entre duas crianças cada uma receberia três doces; quantos doces seriam dados a cada pessoa se não houvesse nenhuma pessoa? II. A divisão por zero iria fazer com que falsas igualdades fossem criadas. Por exemplo,2 · 0 = 3 · 0. Se dividirmos ambos os lados por zero, teríamos 2 =3. III. A divisão com resto pode ser considerada como uma sequência de subtrações: subtrai-se o divisor do dividendo sucessivas vezes até atingir um número menor que o divisor. Por exemplo, ao dividir 7 por 3, subtraímos 3 duas vezes de 7 até chegar em 1; assim o quociente é 2 e o resto é 1. Se subtrairmos zero, nunca seria atingido um número menor que o divisor.
Porém, parte destes argumentos pode levar, erroneamente, à conclusão que ao se dividir um número qualquer não nulo por zero também resultaria em zero. Assinale a alternativa que indica quais destes argumentos podem levar a esta conclusão equivocada.
I. Ao se dividir objetos entre pessoas, como se atribuir algo a nenhuma pessoa? Por exemplo, ao se dividir seis doces entre duas crianças cada uma receberia três doces; quantos doces seriam dados a cada pessoa se não houvesse nenhuma pessoa? II. A divisão por zero iria fazer com que falsas igualdades fossem criadas. Por exemplo,2 · 0 = 3 · 0. Se dividirmos ambos os lados por zero, teríamos 2 =3. III. A divisão com resto pode ser considerada como uma sequência de subtrações: subtrai-se o divisor do dividendo sucessivas vezes até atingir um número menor que o divisor. Por exemplo, ao dividir 7 por 3, subtraímos 3 duas vezes de 7 até chegar em 1; assim o quociente é 2 e o resto é 1. Se subtrairmos zero, nunca seria atingido um número menor que o divisor.
Porém, parte destes argumentos pode levar, erroneamente, à conclusão que ao se dividir um número qualquer não nulo por zero também resultaria em zero. Assinale a alternativa que indica quais destes argumentos podem levar a esta conclusão equivocada.
Considere a função 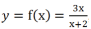 , para x ≠ 2. Assinale a alternativa que apresenta a função g(y) que é a função inversa de f(x).
, para x ≠ 2. Assinale a alternativa que apresenta a função g(y) que é a função inversa de f(x).
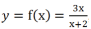 , para x ≠ 2. Assinale a alternativa que apresenta a função g(y) que é a função inversa de f(x).
, para x ≠ 2. Assinale a alternativa que apresenta a função g(y) que é a função inversa de f(x). O consumo atual de água em uma cidade é 53.000.000 l/h. Suponha que este consumo cresça anualmente em 1,75 milhões l/h, e que este crescimento possa ser considerado como uma progressão aritmética. Se a capacidade de produção de água for de 78 mil m³ /h, assinale a alternativa que apresenta em quantos anos, no máximo, será necessária a ampliação da capacidade de produção de água para que não ocorra falta de água.
Considere as expressões abaixo:
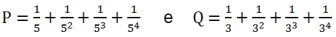
A relação aproximada entre os valores de P e Q é: