2. Questões de Concurso
  3. Questões da Prova
Portal Estadual de Concursos - 2013 - CBM-MS - Soldado do Corpo de Bombeiro
limpar filtros
Questões por página:
Das 150 pessoas aprovadas em um concurso público, sabe-se que 135 são homens,30 cursam ou concluíram curso superior e exatamente 10 mulheres concluíram apenas o ensino médio. Tomando-se aleatoriamente um dos nomes da lista de aprovados, a probabilidade de que a pessoa sorteada seja um homem que esteja cursando ou tenha concluído um curso superior é igual a:

Observe a figura a seguir.

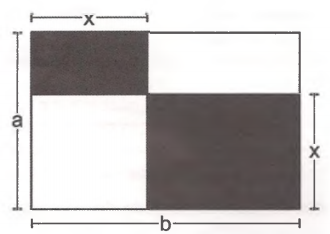
Imagem associada para resolução da questão

No retângulo de dimensões axb foram delimitadas duas regiões ciaras: uma, quadrada de lados iguais a x (0 < x < a), e outra, retangular, de dimensões iguais a a - x e b - x. Entendendo x como uma medida variável no intervalo indicado acima, é possível determinar a área da região escura da figura como uma função S(x).

Sendo assim, considere as seguintes proposições:

I - S(x) = (a + b)x - 2x2. II - S(x) atinge seu valor mínimo para x = (a + b)/4. III - O mínimo valor da função S(x) é (a + b)2/8. IV - Para x = b - a, o valor da função S(x) é igual a 4ab - 3a2 - b2. Das proposições acima:
Alcebíades e Zebedeu, em exercícios de tiro das quais participaram, apresentaram excelentes performances: Alcebíades errou o alvo em apenas 4% dos disparos efetuados e, Zebedeu, em apenas 5% de seus disparos. Em uma competição de tiro em que estão ambos inscritos, esperase desempenhos semelhantes aos obtidos nos exercícios. Sendo assim, ao dispararem uma vez cada um, espera-se que a probabilidade de que Alcebíades erre o alvo e Zebedeu o acerte é:
Um polinómio p(x) é divisível por x - 1, por x + 1 e por x - 2. Sabendo-se que seu grau é o menor possível e que p(3) = 16, então P(0) vale:
O reticulado a seguir representa as quadras de parte de uma cidade, onde não há vias de mão única.
Imagem associada para resolução da questão

Uma viatura de combate a incêndios deve deslocar-se rapidamente do ponto A, sua base, ao ponto B, local de uma ocorrência a ser atendida. Supondo que a viatura cumpra o menor percurso possível, o número de formas como isso pode ser feito é igual a:
© 2016-2024 Fonte Concursos - Questões de Concurso e Plano de Estudo