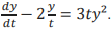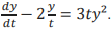Questões da prova:
IDECAN - 2022 - PC-BA - Perito Criminal de Polícia Civil
limpar filtros
100 Questões de concurso encontradas
Página 8 de 20
Questões por página:
Questões por página:
Concurso:
PC-BA
Disciplina:
Estatística
Uma das formulas de calcular a curtose é dada por

• C < 0,263 ➝ Curva Leptocúrtica. • C = 0,263 ➝ Curva Mesocúrtica. • C > 0,263 ➝ Curva Plasticúrtica.
Sabendo que a distribuição apresenta as seguintes medidas Q3 = 40,5; Q1 = 25; P10 = 19,3 e P90 = 49,8.
Determine o valor que aproxima de C e qual tipo de curva.

• C < 0,263 ➝ Curva Leptocúrtica. • C = 0,263 ➝ Curva Mesocúrtica. • C > 0,263 ➝ Curva Plasticúrtica.
Sabendo que a distribuição apresenta as seguintes medidas Q3 = 40,5; Q1 = 25; P10 = 19,3 e P90 = 49,8.
Determine o valor que aproxima de C e qual tipo de curva.
Concurso:
PC-BA
Disciplina:
Raciocínio Lógico
Sejam A e B dois conjuntos, dados da seguinte forma:
A = {8,0; 9,2; 10,0; 8,8; 9,0; 9,0} B = {1,63; 1,65; 1,72; 1,75; 1,79; 1,80; 1,82; 1,83}
Determine o valor da média aritmética e mediana, respectivamente dos conjuntos A e B.
A = {8,0; 9,2; 10,0; 8,8; 9,0; 9,0} B = {1,63; 1,65; 1,72; 1,75; 1,79; 1,80; 1,82; 1,83}
Determine o valor da média aritmética e mediana, respectivamente dos conjuntos A e B.
Concurso:
PC-BA
Disciplina:
Estatística
Sobre a técnica de amostragem estratificada, assinale o item correto.
Concurso:
PC-BA
Disciplina:
Estatística
Sobre probabilidade, analise os itens a seguir:
I. Chamamos de espaço amostra, e indicamos por Ω, umconjunto formado por todos os resultados possíveis de umexperimento aleatório. II. Considerando um experimento aleatório, cujo espaço amostralé Ω. Chamaremos de evento todo subconjunto de Ω.
I. Chamamos de espaço amostra, e indicamos por Ω, umconjunto formado por todos os resultados possíveis de umexperimento aleatório. II. Considerando um experimento aleatório, cujo espaço amostralé Ω. Chamaremos de evento todo subconjunto de Ω.
III. Sejam A e B dois eventos, se A ∩ B = ø, A e B sãochamados mutuamente excludentes.
Assinale
Concurso:
PC-BA
Disciplina:
Matemática
Determine a solução geral da seguinte equação de Bernoulli, dada por