Questões de Concurso
Filtrar
745 Questões de concurso encontradas
Página 127 de 149
Questões por página:
Questões por página:
Concurso:
PM-AC
Disciplina:
Matemática
A febre amarela é uma doença infecciosa aguda, de curta duração (no máximo 10 dias), gravidade variável, causada pelo vírus da febre amarela, que ocorre na América do Sul e na África. A única forma de evitar a febre amarela silvestre é a vacinação contra a doença. A vacina é gratuita e está disponível nos postos de saúde em qualquer época do ano. Disponível em:<http://bvsms.saude.gov.br/bvs/febreamarela/sobre.php> Acesso em 22 mar.2017
Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial? (Use: log 2 = 0,3)
Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial? (Use: log 2 = 0,3)
Dada a função 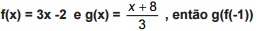 é:
é:
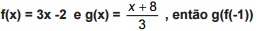 é:
é: Um comerciante separou suas moedas de dez centavos e vinte e cinco centavos e verificou que haviam 65 moedas e um total de R$ 12,80. Desse modo, o valor total das moedas de vinte e cinco centavos é:
Concurso:
Prefeitura de Porto Calvo - AL
Disciplina:
Matemática
Ponto fixo
Em Matemática, define-se ponto fixo como o ponto que não é alterado por uma aplicação (função). Mais precisamente falando, se f:ℜ --> ℜ é uma função, um ponto fixo de f é todo ponto x* tal que f(x*) = x*: Disponível em:<https://pt.wikipedia.org/wiki/Ponto_fixo> . Acesso em: 07 set.2018.
Dadas as afirmativas a respeito de pontos fixos de funções,
I. A função f(x) = x2 + 1 não tem ponto fixo. II. A função f(x) = 2x – 1 tem dois pontos fixos. III. A função f(x) = x3 + x tem um único ponto fixo.
verifica-se que está(ão) correta(s)
Em Matemática, define-se ponto fixo como o ponto que não é alterado por uma aplicação (função). Mais precisamente falando, se f:ℜ --> ℜ é uma função, um ponto fixo de f é todo ponto x* tal que f(x*) = x*: Disponível em:<https://pt.wikipedia.org/wiki/Ponto_fixo> . Acesso em: 07 set.2018.
Dadas as afirmativas a respeito de pontos fixos de funções,
I. A função f(x) = x2 + 1 não tem ponto fixo. II. A função f(x) = 2x – 1 tem dois pontos fixos. III. A função f(x) = x3 + x tem um único ponto fixo.
verifica-se que está(ão) correta(s)
Concurso:
Prefeitura de Porto Calvo - AL
Disciplina:
Matemática
Ponto fixo
Em Matemática, define-se ponto fixo como o ponto que não é alterado por uma aplicação (função). Mais precisamente falando, se f: ℝ→ ℝ é uma função, um ponto fixo de f é todo ponto x* tal que f(x*) = x*:
Disponível em:<https://pt.wikipedia.org/wiki/Ponto_fixo> . Acesso em: 07 set.2018.
Dadas as afirmativas a respeito de pontos fixos de funções,
I. A função f(x) = x2 + 1 não tem ponto fixo.
II. A função f(x) = 2x – 1 tem dois pontos fixos.
III. A função f(x) = x3 + x tem um único ponto fixo.
verifica-se que está(ão) correta(s)