Questões de Concurso

Uma pesquisa afirma que a proporção p de crianças vacinadas, na faixa etária de zero a cinco anos, contra uma determinada doença é igual a 64% na cidade X. Desejando-se por à prova tal afirmação, selecionou-se aleatoriamente 100 crianças da faixa etária estipulada com o objetivo de se testar a (hipótese nula) H₀: p = 0,64 contra a (hipótese alternativa) H₁: p = 0,50. Supondo como estatística apropriada ao teste a frequência relativa de sucessos (sendo sucesso a criança ter sido vacinada) cuja distribuição pode ser aproximada por uma distribuição normal, o valor observado dessa estatística para que a probabilidade do erro do tipo I seja igual à probabilidade do erro do tipo II pertence ao intervalo

Um modelo de regressão linear múltipla tem a forma y = β₀ + β₁X₁ + β₂X₂ + ε, em que β₀, β₁ e β₂ são os coeficientes do modelo e ε denota o erro aleatório normal com média nula e desvio padrão σ. As variáveis regressoras X₁ e X₂ são ortogonais. O quadro a seguir mostra as estimativas dos coeficientes do modelo obtidas pelo método da máxima verossimilhança a partir de uma amostra de tamanho n = 20. Nesse quadro, para cada coeficiente β_k, k = 0,1,2, a razão t refere-se ao seu teste de significância H₀ : β_k = 0 versus H₁ : β_k ≠ 0.

 

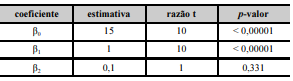
Com base nessas informações e no quadro apresentado, julgue o próximo item.

A hipótese nula H₀ : β₂ = 0 é rejeitada para o nível de significância do teste α = 5%.

Um modelo de regressão linear foi ajustado para explicar os sintomas de transtornos mentais (T) em função da violência intrafamiliar (V) e do inventário do clima familiar (C). A forma desse modelo é dada por T = b₀ + b₁V + b₂C + ε, em que ε representa o erro aleatório normal com média zero e desvio padrão σ, e b₀, b₁ e b₂ são os coeficientes do modelo. A tabela a seguir mostra os resultados da análise de variância (ANOVA) do referido modelo.

Com base na tabela e nas informações apresentadas, julgue o item a seguir

Com relação ao teste linear geral, a hipótese nula H₀ : b₁ = b₂ = 0 não seria rejeitada caso fosse escolhido para esse teste um nível de significância igual ou superior a 1%.

Acerca de métodos usuais de estimação intervalar, julgue o item subsecutivo.

Um intervalo de confiança de 95% descreve a probabilidade de um parâmetro estar entre dois valores numéricos na próxima amostra não aleatória a ser coletada.

Acerca de métodos usuais de estimação intervalar, julgue o item subsecutivo.

É possível calcular intervalos de confiança para a estimativa da média de uma distribuição normal, representativa de uma amostra aleatória