Questões de Concurso

Sobre as variáveis serem discretas ou contínuas, analise as afirmativas abaixo, dê valores Verdadeiro (V) ou Falso (F).

( ) A contagem do número de alunos dentro de uma sala de aula só pode ser uma variável discreta, pois é um número inteiro racional e positivo.

( ) A contagem da quilometragem de um corredor em uma pista circular é uma variável contínua, pois este valor pode assumir qualquer valor dentro do intervalo real, no caso múltiplos de π (pi).

( ) O caso do termômetro analógico (de mercúrio), a variável representada nele é uma variável discreta, pois aceita todos os valores intermediários entre duas temperaturas a e b.

Assinale a alternativa que traga, de cima para baixo, a sequência correta.

Considerando que X₁, X₂, ..., X_n forem variáveis aleatórias independentes, com funções geradoras de momento respectivamente definidas por 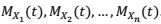. Se Y = X₁ + X₂ + ... + X_n, então a função geradora de momento de Y será dada por:

Considerando que Z e W sejam variáveis aleatórias independentes que seguem distribuição normal padrão, julgue o item subsequente.

Var(2Z + 3W) < 10.

Considerando que Z e W sejam variáveis aleatórias independentes que seguem distribuição normal padrão, julgue o item subsequente.

A transformação 6Z + 3 resulta em uma distribuição normal com variância igual a 9.