Questões de Concurso

Seja X uma variável aleatória normalmente distribuída com média µ e variância populacional desconhecida. Deseja-se testar a hipótese em que a média µ da população, considerada de tamanho infinito, é superior a 20, ao nível de significância de 5%. Para testar a hipótese, foi extraída uma amostra aleatória de 9 elementos, apurando-se uma média igual a 21 e com a soma dos quadrados destes elementos igual a 3.987. As hipóteses formuladas foram H₀: µ = 20 (hipótese nula) e H₁: µ > 20 (hipótese alternativa). Utilizando o teste t de Student, obtém-se que o valor da estatística t_c (t calculado), para ser comparado com o t tabelado, é igual a

A população das medidas dos comprimentos de um tipo de cabo é considerada normalmente distribuída e de tamanho infinito. Seja µ a média desta população com uma variância populacional igual a 2,56 m². Uma amostra aleatória de 64 cabos apresentou um intervalo de confiança de (1-α), em metros, igual a [61,6 ; 62,4]. Se na distribuição normal padrão (Z) a probabilidade P(z> z) = α/2, então z é igual a

Uma população X tem uma função densidade dada por 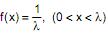Por meio de uma amostra aleatória de 10 elementos de X, obteve-se, pelo método da máxima verossimilhança, uma estimativa para a média de X igual a 4,5. Com base neste resultado, tem-se que a respectiva estimativa da variância de X é igual a

Admite-se que o tempo (t) de funcionamento sem falhas, em horas, de um determinado equipamento obedece a uma lei com função densidade f(t) = λe^-λt ( t > 0 ). Sabe-se que um conjunto de 200 destes equipamentos escolhidos aleatoriamente forneceu a seguinte distribuição:

Utilizando o Método dos Momentos, tem-se que o valor da estimativa de λ é igual a