Questões de Concurso

Considere os estimadores não viezados E’ e E’’ da média µ, dados abaixo, de uma população normal com variância unitária. (X, Y, Z) corresponde a uma amostra aleatória de tamanho 3 da população com m e n sendo parâmetros reais.

E’ = mX + (m - n)Y + (2m - n)Z
E’’ = mX + (3m - n)Y + mZ

É correto afirmar que

Em uma distribuição de valores determinando uma curva de frequência unimodal, verificou-se que o valor da mediana é superior ao valor da moda e inferior ao valor da média. Considere as seguintes informações:

I. A curva possui a cauda mais alongada à direita.

II. A distribuição é assimétrica à direita.

III. A amplitude do intervalo entre a moda e a mediana é inferior à amplitude do intervalo entre a mediana e a média.

IV. Os valores da distribuição estão fortemente concentrados em torno da mediana.

V. Metade dos valores da distribuição situam-se entre o valor da moda e o valor da média.

O número de assertivas corretas é igual a

Duas empresas X e Y possuem 150 e 100 empregados, respectivamente. A média aritmética dos salários da empresa X supera a da empresa Y em R$ 500,00 e o desvio padrão da empresa X supera o da empresa Y em R$ 200,00. Se os coeficientes de variação das empresas X e Y são respectivamente iguais a 20% e 15%, então a média aritmética de todos os empregados das empresas X e Y, em conjunto, apresenta o valor de

Os preços unitários de venda de um determinado equipamento no mercado estão distribuídos conforme representação do histograma abaixo. No eixo das ordenadas constam as respectivas densidades de frequências em (R$ 1.000,00)^-1. Define-se densidade de frequência de um intervalo de classe como sendo o quociente da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.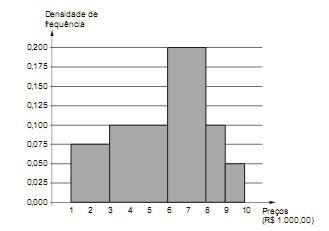



Considerando os intervalos de classe fechados à esquerda e abertos à direita, obtém-se que a porcentagem dos preços unitários, que são iguais ou superiores a R$ 3.000,00 e inferiores a R$ 8.000,00, corresponde a

A tabela de frequências relativas abaixo corresponde à distribuição da renda mensal das pessoas que adquiriram pacotes de excursão de uma empresa de turismo em 2010. O valor da média aritmética da renda (Me) foi obtido considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo. O valor da mediana (Md) foi obtido pelo método da interpolação linear.



O valor da moda (Mo), obtido pela relação de Pearson: Mo = 3Md - 2Me, é igual a