Em um levantamento realizado em uma grande empresa com 400 de seus empregados, escolhidos aleatoriamente, obteve-se a seguinte tabela com relação à preferência por 4 candidatos X, Y, Z e T para presidente do sindicato.



Deseja-se testar com base nesta tabela, utilizando o teste qui-quadrado, as seguintes hipóteses:

H₀: não há discrepância entre as frequências observadas e esperadas (hipótese nula).
H₁: as frequências observadas e esperadas são discrepantes (hipótese alternativa).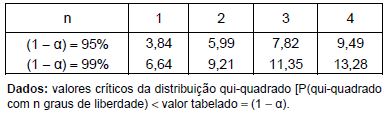



Uma conclusão correta é que

Em uma empresa foram selecionados aleatoriamente 256 empregados que se submeteram a um treinamento durante 30 dias. Verificando que x empregados apresentaram melhora no desempenho após o treinamento, decidiu-se utilizar o teste do sinal, atribuindo x sinais positivos para os empregados que melhoraram e (256 - x) sinais negativos para os restantes. Aplicando então o teste do sinal para decidir se a proporção populacional de sinais positivos (p) é igual a 50%, a um nível de significância de 5%, foram formuladas as hipóteses H₀ : p = 50% (hipótese nula) contra H₁ : p ≠ 50% (hipótese alternativa). Com a aproximação da distribuição binomial pela normal, sem a correção de continuidade, foi apurado o valor do escore reduzido r correspondente para comparação com o valor crítico z da distribuição normal padrão Z tal que a probabilidade  P( |Z| ≤ z) = 95%.Se r = 2,5, então x é igual a

Deseja-se testar, ao nível de significância de 5%, se a média µ de uma população normal de tamanho infinito e variância populacional igual a 400 é diferente de 100. Para isto, foi extraída uma amostra aleatória desta população de tamanho igual a 64, encontrando-se uma média amostral igual a M. Foram formuladas as hipóteses H₀ : µ = 100 (hipótese nula) e H₁ : µ = 100 (hipótese alternativa). Considere que na curva normal padrão Z as probabilidades P(Z > 1,96) = 0,025, P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10. O menor valor encontrado para M, a partir do qual H₀ não é rejeitada, é

Em uma grande cidade é realizada uma pesquisa com 400 eleitores, escolhidos aleatoriamente, sobre o nível de satisfação do atual prefeito e 80% deles classificaram como “Bom”. Deseja-se construir um intervalo de confiança de 95% para esta proporção com base neste levantamento supondo que é normal a distribuição amostral da frequência relativa dos eleitores que consideram o nível de satisfação como “Bom”. Dado que na distribuição normal padrão Z as probabilidades P(Z > 1,96) = 0,025, P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10, obtém-se que o intervalo, em %, é igual a

Uma população, considerada de tamanho infinito, apresenta uma distribuição normal com média µ e uma variância populacional igual a 576. Com base em uma amostra aleatória de tamanho 100 extraída desta população, obteve-se um intervalo de confiança para µ igual a [194,48 ; 205,52], com um nível de confiança de (1 - ∝ ). Considerando uma outra amostra aleatória desta população, independente da primeira, de tamanho 144 obteve-se um novo intervalo de confiança para µ com um nível de confiança (1 - ∝ ). A amplitude deste novo intervalo é igual a