mostrar texto associado esconder texto associado

Aplicando uma realimentação de estado, com a lei de controle dada por τ(t)= - KX(t)= -[k₁ k₂] X(t), o valor do vetor de ganhos K, que conduz os polos em malha fechada para as posições -2 e -3, é

Um sistema de 2ª ordem é dado pela sua função de transferência  G(s) = 64 /s² + 8s +64. Sabe-se que o tempo de subida, medido sobre a curva de resposta ao degrau aplicado nesse sistema, é dado por T_R = π -Φ /ωn , onde

•ζ = cos (Φ) é a razão de amortecimento; e

• ωⁿ é a frequência natural não amortecida.

Para discretizar esse sistema e aplicar um controle digital, o período de amostragem deve ser tal que ocorram 10 amostras durante o tempo de subida. O valor aproximado desse período é

O modelo discreto de um sistema, em malha aberta, é representado pela função de transferência G(z) = K(z +1) / z² -1,5z + 0,5. A figura acima mostra o esboço do lugar das raízes, no plano Z, para esse sistema, em malha fechada, com realimentação de saída e com o ganho variando no intervalo 0 ≤ k < + ∞ . O circulo unitário está traçado com linha pontilhada. O valor do ganho K, para que o sistema em malha fechada esteja no limiar da instabilidade, é

Um sistema discreto de 2ª ordem é composto por dois polos complexos, conjugados, que estão representados no diagrama de polos e zeros da figura acima. O círculo unitário está traçado com linha pontilhada. A resposta ao impulso desse sistema gera um sinal, discreto, senoidal amortecido e que oscila na frequência de 25π rad/s. Nessas condições, o período de amostragem, em ms, usado na discretização desse sistema, é

A figura acima mostra dois sinais, na forma de pulsos limitados no tempo. Considere que a transformada de Fourier de v(t) é dada pela expressão, na forma polar, 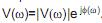. Com base nas propriedades da transformada de Fourier e considerando as semelhanças e simetrias entre os dois pulsos, a expressão da transformada de w(t) é