2. Questões de Concurso
  3. Questões do Concurso
ANAC - 2015
limpar filtros
Questões por página:
Ao se determinar a taxa de chegadas de passageiros preferenciais (λ1 ) e passageiros não preferenciais (λ2 ) no guichê de uma companhia aérea, observou-se que a taxa de chegadas dos passageiros preferenciais é igual a dois passageiros por minuto (λ1 = 2) e a taxa de chegadas dos passageiros não preferenciais é igual a três passageiros por minuto (λ2 = 3). Além disso, observou-se que estas duas chegadas ocorrem de acordo com um processo de Poisson. Indique qual a probabilidade de que exatamente cinco passageiros, P(X=5), contando os passageiros preferenciais e os não preferenciais, chegarão ao guichê no intervalo de um minuto (caso seja necessário, use o valor de e=exp(1) = 2,72).

A probabilidade de haver atraso em um voo em um determinado aeroporto em uma hora é dada pela seguinte função de densidade de probabilidade f(x):



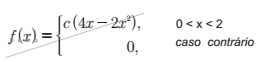
Pede-se para determinar o valor de c para a função de densidade probabilidade f(x) acima e indicar qual a probabilidade de P(0<x<1).

Considere o seguinte processo auto regressivo de segunda ordem: yt = a0 + a2 yt-2 + εt ., onde | a2 | < 1. A partir desta equação, de segunda ordem, encontre Et-2yt e Et-1yt.
Uma distribuição Binomial pode ser aproximada por uma distribuição de Poisson, quando a probabilidade do evento é pequena de ocorrer e a população considerada é relativamente grande. Assuma esta aproximação para o problema descrito a seguir. Considere que passageiros chegam a um aeroporto a uma taxa média de três passageiros por segundo. Pede-se para determinar, com uma boa aproximação, qual a probabilidade (P) de que não mais de dois passageiros chegarão ao aeroporto em um intervalo de um segundo (caso seja necessário, use o valor de e=exp(1) = 2,72).

Um estudo foi realizado para investigar a resistência do solo (y) ao cisalhamento quando relacionado à profundidade (x1), dada em centímetros, e ao conteúdo de umidade (x2) dado em %. Dez observações foram realizadas, e as seguintes grandezas foram obtidas: n=10, . Pede-se para estabelecer as equações de mínimos quadrados para o modelo: Y = α0 +α1  x1 +α2  x2 +ε.

© 2016-2024 Fonte Concursos - Questões de Concurso e Plano de Estudo