916 Questões de concurso encontradas
Página 73 de 184
Questões por página:
Um teste de hipótese será feito com base numa distribuição normal, com média desconhecida e variância σ2 =64 Uma amostra de tamanho n = 16 é extraída e sua média calculada, sendo X = 7 O conjunto de hipóteses a ser testado é:
Considere ainda que a região crítica do teste é RC = (9, + ∞) que, caso Ho seja falsa, o μ verdadeiro seria igual a 8.Além disso, são fornecidos os seguintes dados sobre a função distribuição acumulada da normal-padrão.
Φ(0,5) ≅ 0,69 Φ(1) ≅ 0,84 Φ(1,5) ≅ 0,93 Φ(2) ≅ 0,98
Logo, as probabilidades dos erros do Tipo I, do Tipo II e do p-valor (bilateral) do teste são, respectivamente, iguais a:
Com o objetivo de estimar, por intervalo, a verdadeira média populacional de uma distribuição, é extraída uma amostra aleatória de tamanho n = 26. Sendo a variância desconhecida, calcula-se o valor de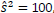 
além da média amostral X = 8 de grau de confiança pretendido é de 95%. Somam-se a todas essas informações os valores tabulados:
Φ(1,65) ≅ 0,95 Φ(1,96) ≅ 0,975 T25(1,71) ≅ 0,95
T26(1,70) ≅ 0,95 T25(2,06) ≅ 0,975 T26(2,05) ≅ 0,975
Onde, 
= estimador não-viesado da variância populacional;
Φ(z) = fç distribuição acumulada da Normal-padrão;
Tn(t)= fç distribuição acumulada da T-Student com n graus de liberdade.
Então os limites do intervalo de confiança desejado são:
Considere os estimadores a seguir, tendo em vista a média populacional μ, a partir de uma amostra de tamanho n.
Se a variância populacional é finita, sobre as propriedades d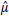e 
e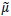 
correto afirmar que:
Para estimar, por máxima verossimilhança (MV) ou pelo método dos momentos (MM), o único parâmetro de dada distribuição de probabilidades, seleciona-se uma amostra de tamanho n.
A função densidade da distribuição é:
fx(x) = θxθ-1 , para 0 < x < 1 e zero caso contrário.Além disso, considere:
Então, os estimadores de MV e de MM (com base na média da distribuição) para θ são, respectivamente:
