Questões do concurso:
Banco da Amazônia - 2012 - Técnico Científico e de Técnico Bancário
limpar filtros
1.710 Questões de concurso encontradas
Página 130 de 342
Questões por página:
Questões por página:
Concurso:
Banco da Amazônia
Disciplina:
Estatística
mostrar texto associado
A função de densidade espectral f(λ) representa o espaço de estados de um processo estocástico no domínio de Fourier.
Para um processo AR(1), é correto afirmar que essa função é expressa na forma f(λ) = σ x { 2π ( 1-2Φcosλ ) } -1, em que |λ| ≤ π e |Φ| > 1.
Para um processo AR(1), é correto afirmar que essa função é expressa na forma f(λ) = σ x { 2π ( 1-2Φcosλ ) } -1, em que |λ| ≤ π e |Φ| > 1.
Concurso:
Banco da Amazônia
Disciplina:
Estatística
mostrar texto associado
O modelo ARIMA(3, 1, 2) é um filtro linear que permite descrever uma série temporal estacionária com período sazonal igual a 3.
Concurso:
Banco da Amazônia
Disciplina:
Estatística
mostrar texto associado
Considere que uma sequência de números seja gerada de acordo com a seguinte fórmula: Xn + 1 = (aXn + b) mod w. Nesse caso, o valor a deve ser escolhido de modo que se garanta um longo ciclo de números pseudoaleatórios, isto é, o valor a determina o tamanho do ciclo do algoritmo.
Concurso:
Banco da Amazônia
Disciplina:
Estatística
mostrar texto associado
Para a geração de realizações de duas variáveis X e Y, os amostrados de Gibbs consideram alternadamente as distribuições condicionais X|Y = y e Y|X = x. Assim, é correto afirmar que, se X segue uma distribuição de Bernoulli com parâmetro Y e se Y segue uma distribuição Beta com parâmetros a e b, então a distribuição conjunta da amostra gerada pelo amostrador de Gibbs segue aproximadamente uma distribuição Beta com parâmetros a + X e b + 1 – X.
Concurso:
Banco da Amazônia
Disciplina:
Estatística
mostrar texto associado
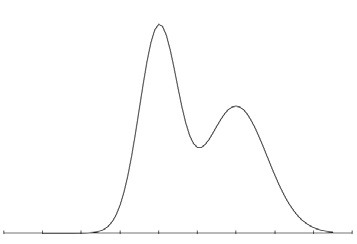
Considere que a função densidade de probabilidade de certa variável aleatória possua o gráfico ilustrado na figura abaixo.
Nesse caso, se o algoritmo EM (expectation-maximization) for aplicado a essa distribuição, independentemente do lado da cauda de início, o algoritmo convergirá para o ponto de máximo global da distribuição.